
【題目】已知函數(shù)![]() (
(![]() 且
且![]() ).
).
(1)求函數(shù)![]() 的定義域,并求出當
的定義域,并求出當![]() 時,常數(shù)
時,常數(shù)![]() 的值;
的值;
(2)在(1)的條件下,判斷函數(shù)![]() 在
在![]() 的單調性,并用單調性定義證明;
的單調性,并用單調性定義證明;
(3)設![]() ,若方程
,若方程![]() 有實根,求
有實根,求![]() 的取值范圍.
的取值范圍.
 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源: 題型:
【題目】有甲乙兩個班級進行數(shù)學考試,按照大于等于85分為優(yōu)秀,85分以下為非優(yōu)秀統(tǒng)計成績后,得到如下的列聯(lián)表.
| 優(yōu)秀 | 非優(yōu)秀 | 總計 |
甲班 | 10 | ||
乙班 | 30 | ||
總計 | 105 |
已知在全部105人中隨機抽取1人為優(yōu)秀的概率為![]() .
.
(1)請完成上面的列聯(lián)表;(把列聯(lián)表自己畫到答題卡上)
(2)根據(jù)列聯(lián)表的數(shù)據(jù),若按95%的可靠性要求,能否認為“成績與班級有關系”?
參考公式:![]()
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)求證:數(shù)列![]() 是等差數(shù)列,求數(shù)列
是等差數(shù)列,求數(shù)列![]() 的通項公式;
的通項公式;
(3)若![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】給定一個由![]() 個小正方形拼成的棋盤形方格,這些小正方形的顏色黑白相間(如圖).
個小正方形拼成的棋盤形方格,這些小正方形的顏色黑白相間(如圖).
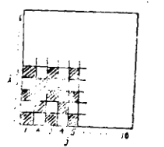
現(xiàn)定義一種運算A:把位于第i行的所有小正方形和位于第j列的所有小正方形都換成相反的顏色,即黑色的小正方形換成白色的,白色的小正方形換成黑色的,這里![]() .我們把A稱為在位于第i行第j列上的小正方形上的一次運算.試問:能否經過若干次上述運算把棋盤上的所有小正方形全部換成同一種顏色?證明你的結論.
.我們把A稱為在位于第i行第j列上的小正方形上的一次運算.試問:能否經過若干次上述運算把棋盤上的所有小正方形全部換成同一種顏色?證明你的結論.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)f(x)=Asin(wx+j)(A>0,w>0,-![]() <j<
<j<![]() ,x∈R)的部分圖象如圖所示:
,x∈R)的部分圖象如圖所示: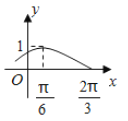 ,
,
(1)求函數(shù)y=f(x)的解析式;(2)當x∈![]() 時,求f(x)的取值范圍.
時,求f(x)的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某校研究性學習小組從汽車市場上隨機抽取![]() 輛純電動汽車調查其續(xù)駛里程(單次充電后能行駛的最大里程),被調查汽車的續(xù)駛里程全部介于
輛純電動汽車調查其續(xù)駛里程(單次充電后能行駛的最大里程),被調查汽車的續(xù)駛里程全部介于![]() 公里和
公里和![]() 公里之間,將統(tǒng)計結果分成
公里之間,將統(tǒng)計結果分成![]() 組:
組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,繪制成如圖所示的頻率分布直方圖.
,繪制成如圖所示的頻率分布直方圖.
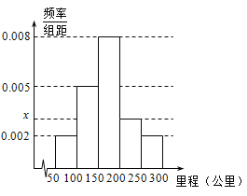
(1)求直方圖中![]() 的值;
的值;
(2)求![]() 輛純電動汽車續(xù)駛里程的中位數(shù);
輛純電動汽車續(xù)駛里程的中位數(shù);
(3)若從續(xù)駛里程在![]() 的車輛中隨機抽取
的車輛中隨機抽取![]() 輛車,求其中恰有一輛車的續(xù)駛里程為
輛車,求其中恰有一輛車的續(xù)駛里程為![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某高中為了了解高三學生每天自主參加體育鍛煉的情況,隨機抽取了100名學生進行調查,其中女生有55名.下面是根據(jù)調查結果繪制的學生自主參加體育鍛煉時間的頻率分布直方圖:
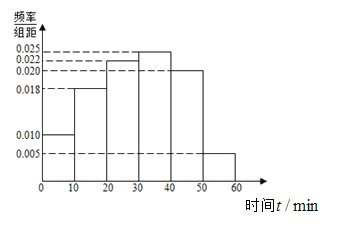
將每天自主參加體育鍛煉時間不低于40分鐘的學生稱為體育健康A類學生,已知體育健康A類學生中有10名女生.
(Ⅰ)根據(jù)已知條件完成下面![]() 列聯(lián)表,并據(jù)此資料你是否認為達到體育健康A類學生與性別有關?
列聯(lián)表,并據(jù)此資料你是否認為達到體育健康A類學生與性別有關?
非體育健康A類學生 | 體育健康A類學生 | 合計 | |
男生 | |||
女生 | |||
合計 |
(Ⅱ)將每天自主參加體育鍛煉時間不低于50分鐘的學生稱為體育健康![]() 類學生,已知體育健康
類學生,已知體育健康![]() 類學生中有2名女生,若從體育健康
類學生中有2名女生,若從體育健康![]() 類學生中任意選取2人,求至少有1名女生的概率.
類學生中任意選取2人,求至少有1名女生的概率.
附:
P( | 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
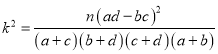
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】同時具有性質:“① 最小正周期是![]() ;② 圖象關于直線
;② 圖象關于直線![]() 對稱;③ 在
對稱;③ 在![]() 上是單調遞增函數(shù)”的一個函數(shù)可以是( )
上是單調遞增函數(shù)”的一個函數(shù)可以是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com