
分析 (1)求f(x)的導數f′(x),根據x>0求出f'(x)的值域,討論a的值得出f′(x)的正負情況,判斷f(x)的單調性和極值點問題;
(2)(i)f(x)≤g(x)等價于ex-lnx+x2≥ax,由x>0,利用分離常數法求出a的表達式,再構造函數求最值即可;
(ii)由( i)結論,a=e+1時有f(x)≤g(x),得出不等式,再進行等價轉化,證明轉化的命題成立即可.
解答 解:(1)由題意得f'(x)=x+$\frac{1}{x}$+a=$\frac{{x}^{2}+ax+1}{x}$,
當a2-4≤0,即-2≤a≤2時,f'(x)≥0恒成立,無極值點;
當a2-4>0,即a<-2或a>2時,
①a<-2時,設方程x2+ax+1=0兩個不同實根為x1,x2,不妨設x1<x1,x2,
則x1+x2=-a>0,x1x2=1>0,故0<x1<x2,
∴x1,x2是函數的兩個極值點.
②a>2時,設方程x2+ax+1=0兩個不同實根為x1,x2,
則x1+x2=-a<0,x1x2=1>0,故x1<0,x2<0,
故函數沒有極值點.
綜上,當a<-2時,函數有兩個極值點;
當a≥-2時,函數沒有極值點.
(2)(i)f(x)≤g(x)等價于ex-lnx+x2≥ax,
由x>0,即a≤$\frac{{e}^{x}{+x}^{2}-lnx}{x}$對于?x>0恒成立,
設φ(x)=$\frac{{e}^{x}{+x}^{2}-lnx}{x}$(x>0),
φ′(x)=$\frac{{e}^{x}(x-1)+lnx+(x+1)(x-1)}{{x}^{2}}$,
∵x>0,∴x∈(0,1)時,φ'(x)<0,φ(x)單調遞減,
x∈(1,+∞)時,φ'(x)>0,φ(x)單調遞增,
∴φ(x)≥φ(1)=e+1,
∴a≤e+1.
(ii)( ii)由( i)知,當a=e+1時有f(x)≤g(x),
即:ex+$\frac{3}{2}$x2≥lnx+$\frac{1}{2}$x2+(e+1)x,
等價于ex+x2-(e+1)x≥lnx…①當且僅當x=1時取等號,
以下證明:lnx+$\frac{e}{x}$≥2,
設θ(x)=lnx+$\frac{e}{x}$,則θ′(x)=$\frac{1}{x}$-$\frac{e}{{x}^{2}}$=$\frac{x-e}{{x}^{2}}$,
∴當x∈(0,e)時θ'(x)<0,θ(x)單調遞減,
x∈(e,+∞)時θ'(x)>0,θ(x)單調遞增,
∴θ(x)≥θ(e)=2,
∴lnx+$\frac{e}{x}$≥2,②當且僅當x=e時取等號;
由于①②等號不同時成立,故有ex+x2-(e+1)x+$\frac{e}{x}$>2.
點評 本題考查了函數與導數的綜合應用問題,也考查了求函數最值與不等式恒成立問題,是綜合性問題.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:選擇題
| A. | {x|x<0} | B. | {x|-4<x<0} | C. | {x|-4<x<1} | D. | {x|x<1} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{5}$ | B. | -$\frac{7}{5}$ | C. | $-\frac{1}{5}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
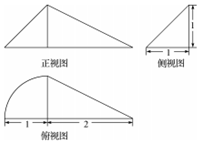
| A. | $\frac{π}{6}+\frac{1}{3}$ | B. | $\frac{π}{12}+1$ | C. | $\frac{π}{12}+\frac{1}{3}$ | D. | $\frac{π}{4}+\frac{1}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2n | B. | 2n | C. | n2 | D. | nn |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
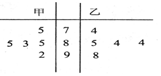 如圖是某班甲、乙兩位同學在5次階段性檢測中的數學成績(百分制)的莖葉圖,甲、乙兩位同學得分的中位數分別為x1,x2,得分的方差分別為y1,y2,則下列結論正確的是( )
如圖是某班甲、乙兩位同學在5次階段性檢測中的數學成績(百分制)的莖葉圖,甲、乙兩位同學得分的中位數分別為x1,x2,得分的方差分別為y1,y2,則下列結論正確的是( )| A. | x1<x2,y1<y2 | B. | x1<x2,y1>y2 | C. | x1>x2,y1>y2 | D. | x1>x2,y1<y2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com