
���}Ŀ����֪����(sh��)![]() ��������
��������![]() ���c(di��n)
���c(di��n)![]() ̎���о����̞�
̎���о����̞�![]() .
.
(1)��(sh��)��(sh��)a��b��ֵ������(sh��)![]() �Ć��{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
(2)���P(gu��n)��x�IJ���ʽ![]() ���������(sh��)��(sh��)m��ȡֵ����.
���������(sh��)��(sh��)m��ȡֵ����.
���𰸡�(1)![]() �����^(q��)�g��
�����^(q��)�g��![]() ���f�p�^(q��)�g��
���f�p�^(q��)�g��![]() ��(2)
��(2) ![]() .
.
��������
��1����֪����(sh��)��ij�c(di��n)̎���о����̣��ɵó����c(di��n)�v����(bi��o)�����о�б�ʣ�����ԭ����(sh��)��ԭ����(sh��)��(d��o)����(sh��)�У�����Ⅲ��(sh��)ֵ���M(j��n)����⺯��(sh��)���{(di��o)�^(q��)�g.
��2��������(sh��)�IJ���ʽ��������}���Ɍ�����(sh��)�����ɲ���ʽһ��(c��)��ȡ�º���(sh��)������ֵ.
(1)��?y��n)?/span>![]() ��
��
������![]() ��
��
��?y��n)�����y=f(x)���c(di��n)(1��f(1))̎���о����̞�2x-y+1=0��
�t��![]() ��
��
��![]() ���a=1��b=2.
���a=1��b=2.
����![]() ��
��
��![]() ����
����![]() �����Ժ���(sh��)
�����Ժ���(sh��)![]() ���{(di��o)�f���^(q��)�g��
���{(di��o)�f���^(q��)�g��![]() ;
;
��![]() ����
����![]() �����Ժ���(sh��)
�����Ժ���(sh��)![]() ���{(di��o)�f�p�^(q��)�g��
���{(di��o)�f�p�^(q��)�g��![]() .
.
(2)���}�⣬����ʽ![]() �������
�������
��![]() �������
�������
��![]() �����.
�����.
��![]() ���tֻ��
���tֻ��![]() ��
��
��![]()
��g'(x)=0����x=1. ....
���Ԯ�(d��ng)x��(0��1)�r(sh��)��g(x) <0;��(d��ng)x��(1��+��)�r(sh��)��g��(x) >0��
����![]() ��
��
����![]() ��������(sh��)��(sh��)m�ķ�����
��������(sh��)��(sh��)m�ķ�����![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() �M�㣺��
�M�㣺��![]() ��
��![]() �����ڮ�(d��ng)
�����ڮ�(d��ng)![]() ��
��![]() ���r(sh��)��
���r(sh��)��![]() ���ۮ�(d��ng)
���ۮ�(d��ng)![]() ��
��![]() ���r(sh��)��
���r(sh��)��![]() ��ӛ��(sh��)��
��ӛ��(sh��)��![]() ��ǰ
��ǰ![]() �(xi��ng)�͞�
�(xi��ng)�͞�![]() .
.
��1����![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2����![]() ����
����![]() ����Сֵ��
����Сֵ��
��3�����C��![]() �ij�Ҫ�l����
�ij�Ҫ�l����![]() ��
��![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����֪�����FP��ABCD������ABCD�����Σ�PA��ƽ��ABCD����ABC��60����E��F�քe��BC��PC�����c(di��n).
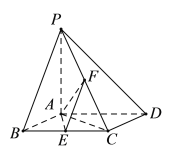
(I)�C����AE��PD��
(II)�O(sh��)AB��PA��2��
������ֱ��PB�cAD���ɽǵ�����ֵ��
��������E��AF��C������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�AC��![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ��
��![]() ���x���ʞ�
���x���ʞ�![]() ���c(di��n)
���c(di��n)![]() �ڙE�AC�ϣ���
�ڙE�AC�ϣ���![]() ��
��![]()
![]() ����F1MF2����e��
����F1MF2����e��![]() .
.
(1)��E�AC�Ę�(bi��o)��(zh��n)���̣�
(2)��ֱ֪��l�c�E�AC����A��B���c(di��n)��![]() ����ֱ��lʼ�K�c�A
����ֱ��lʼ�K�c�A![]() ���У���돽r��ֵ.
���У���돽r��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() �ĸ��(xi��ng)��������(sh��)����ǰ
�ĸ��(xi��ng)��������(sh��)����ǰ![]() �(xi��ng)�͞�
�(xi��ng)�͞�![]() ���ҝM��
���ҝM��![]() ������(sh��)��
������(sh��)��![]() �M��
�M��![]() ���ҵ�ʽ
���ҵ�ʽ![]() ������
������![]() ������
������
��1����(sh��)��![]() ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��
��2������(sh��)��![]() �c
�c![]() ���(xi��ng)���g����(g��u)����(sh��)��
���(xi��ng)���g���И�(g��u)����(sh��)��![]() ���O(sh��)ԓ��(sh��)�О�
���O(sh��)ԓ��(sh��)�О�![]() ����(sh��)��
����(sh��)��![]() ��ͨ�(xi��ng)��ʽ��ǰ
��ͨ�(xi��ng)��ʽ��ǰ![]() �(xi��ng)�ĺ�
�(xi��ng)�ĺ�![]() ��
��
��3�����ڣ�2���еĔ�(sh��)��![]() ǰ
ǰ![]() �(xi��ng)��
�(xi��ng)��![]() ����
����![]() ������
������![]() ����������(sh��)��(sh��)
����������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪?ji��ng)�ֱ��![]() ��ֱ��
��ֱ��![]() �S���c�E�A
�S���c�E�A![]() ����
����![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�![]() .
.
��1�����c(di��n)![]() ��܉�E
��܉�E![]() �ķ��̣�
�ķ��̣�
��2��ֱ��![]() �c�E�A
�c�E�A![]() �ཻ��
�ཻ��![]() ���c����
���c����![]() �������c(di��n)
�������c(di��n)![]() ��
��![]() ������(bi��o)ԭ�c(di��n)����
������(bi��o)ԭ�c(di��n)����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)����![]() �ǽ��c(di��n)��
�ǽ��c(di��n)��![]() �S�ϵęE�A���ɂ�(g��)���c(di��n)�քe����
�S�ϵęE�A���ɂ�(g��)���c(di��n)�քe����![]() ��
��![]() ����
����![]() ��
��![]() �������ϵ�����һ�c(di��n)�����c(di��n)
�������ϵ�����һ�c(di��n)�����c(di��n)![]() ���ɂ�(g��)���c(di��n)���x֮�͞�4.
���ɂ�(g��)���c(di��n)���x֮�͞�4.
��1����![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���O(sh��)![]() ������c(di��n)��
������c(di��n)��![]() ����ֱ��
����ֱ��![]() ��
��![]() �c����
�c����![]() ���ڃ��c(di��n)
���ڃ��c(di��n)![]() ��
��![]() ��
��![]() ��
��![]() ����������c(di��n)�����ҝM��
����������c(di��n)�����ҝM��![]() �����C��ֱ��
�����C��ֱ��![]() ���^���c(di��n)�������ԓ���c(di��n)������(bi��o).
���^���c(di��n)�������ԓ���c(di��n)������(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������˽��\(y��n)��(d��ng)����p�ʵ�Ч����ij�������{(di��o)����20�������ߣ�����֮ǰ�������w����r�����SD��1����ʾ����(j��ng)�^�Ă�(g��)�µĽ������������w����r�������SD��2����ʾ.���Ƚ���ǰ���P(gu��n)���@20�������ߣ�����Y(ji��)Փ�����_���ǣ� ��
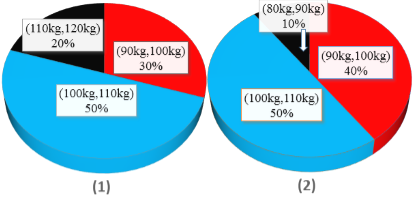
A.�����������w���څ^(q��)�g![]() ��(n��i)����������2��(g��)
��(n��i)����������2��(g��)
B.�����������w���څ^(q��)�g![]() ��(n��i)���˔�(sh��)�]�и�׃
��(n��i)���˔�(sh��)�]�и�׃
C.����������20�˵�ƽ���w�ش�s�p����8 kg
D.����������ԭ���w���څ^(q��)�g![]() ��(n��i)�ķ������w�ض��Мp��
��(n��i)�ķ������w�ض��Мp��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ֱ������(bi��o)ϵ�У��A�ķ��̞�![]() ��
��![]() ��
��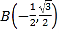 ��
��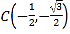 ��A������(g��)���c(di��n)��ijͬ�W(xu��)��
��A������(g��)���c(di��n)��ijͬ�W(xu��)��![]() �c(di��n)�_ʼ���ÔS���ӵķ����Ƅ�(d��ng)���ӣ�Ҏ(gu��)������ÿ�Sһ�����ӣ���һö���ӏ�һ��(g��)���c(di��n)�؈A���Ƅ�(d��ng)��������һ��(g��)���c(di��n)���������Ƅ�(d��ng)�ķ����ɔS���ӛQ�������S�����ӵ��c(di��n)��(sh��)��ż��(sh��)���t���D�м��^�����Ƅ�(d��ng)�����S�����ӵ��c(di��n)��(sh��)���攵(sh��)���t���D�м��^�෴�ķ����Ƅ�(d��ng)���O(sh��)�S����
�c(di��n)�_ʼ���ÔS���ӵķ����Ƅ�(d��ng)���ӣ�Ҏ(gu��)������ÿ�Sһ�����ӣ���һö���ӏ�һ��(g��)���c(di��n)�؈A���Ƅ�(d��ng)��������һ��(g��)���c(di��n)���������Ƅ�(d��ng)�ķ����ɔS���ӛQ�������S�����ӵ��c(di��n)��(sh��)��ż��(sh��)���t���D�м��^�����Ƅ�(d��ng)�����S�����ӵ��c(di��n)��(sh��)���攵(sh��)���t���D�м��^�෴�ķ����Ƅ�(d��ng)���O(sh��)�S����![]() �Εr(sh��)�������Ƅ�(d��ng)��
�Εr(sh��)�������Ƅ�(d��ng)��![]() ��
��![]() ��
��![]() ̎�ĸ��ʷքe��
̎�ĸ��ʷքe��![]() ��
��![]() ��
��![]() �����磺�S����һ�Εr(sh��)�������Ƅ�(d��ng)��
�����磺�S����һ�Εr(sh��)�������Ƅ�(d��ng)��![]() ��
��![]() ��
��![]() ̎�ĸ��ʷքe��
̎�ĸ��ʷքe��![]() ��
��![]() ��
��![]() ��
��
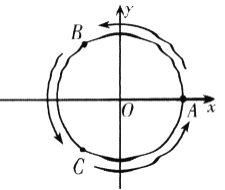
��1���քe�S���Ӷ��Σ����Εr(sh��)�������ӷքe�Ƅ�(d��ng)��![]() ��
��![]() ��
��![]() ̎�ĸ��ʣ�
̎�ĸ��ʣ�
��2���S����![]() �Εr(sh��)������
�Εr(sh��)������![]() �S��ؓ(f��)���S��ʼ߅�����侀
�S��ؓ(f��)���S��ʼ߅�����侀![]() ��
��![]() ��
��![]() ��K߅�Ľǵ�����ֵӛ���S�C(j��)׃��
��K߅�Ľǵ�����ֵӛ���S�C(j��)׃��![]() ����
����![]() �ķֲ��к͔�(sh��)�W(xu��)������
�ķֲ��к͔�(sh��)�W(xu��)������
��3��ӛ![]() ��
��![]() ��
��![]() ������
������![]() ���C������(sh��)��
���C������(sh��)��![]() �ǵȱȔ�(sh��)�У�����
�ǵȱȔ�(sh��)�У�����![]() .
.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com