設x>1,y>1且(x-1)(y-1)=2,若x+y≥k恒成立,則實數k的取值范圍是 .
【答案】
分析:根據題意,x+y≥k可變形為(x-1)+(y-1)+2≥k,只需k小于等于(x-1)+(y-1)+2的最小值即可,令t=(x-1)+(y-1)+2,且(x-1)(y-1)=2,則t=(x-1)+
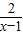
+2,由基本不等式的性質,計算可得答案.
解答:解:根據題意,x+y≥k可變形為(x-1)+(y-1)+2≥k,
只需k小于等于(x-1)+(y-1)+2的最小值即可,
設x>1,y>1,則(x-1)>0,(y-1)>0,
令t=(x-1)+(y-1)+2,且(x-1)(y-1)=2,
則t=(x-1)+
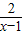
+2≥3+2
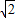
,
則k≤2+2
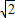
,
故答案為(-∞,2+2
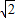
].
點評:本題考查基本不等式的性質與運用,正確運用公式要求“一正、二定、三相等”,解本題時,應注意(x-1)、(y-1)的符號.

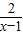 +2,由基本不等式的性質,計算可得答案.
+2,由基本不等式的性質,計算可得答案.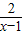 +2≥3+2
+2≥3+2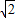 ,
,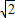 ,
,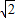 ].
].
