分析:在同一平面直角坐標系中,畫出函數y=lgx與y=-x+3的圖象.它們的交點橫坐標x0,顯然在區間(1,3)內,由于畫圖精確性的限制,單憑直觀就比較困難了.實際上這是要比較x0與2的大小.當x=2時,lgx=lg2,3-x=1.由于lg2<1,因此x0>2,從而得到答案.
解答: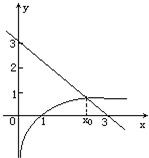
解:lgx+x-3=0可化為:lgx=-x+3,
在同一平面直角坐標系中,畫出函數y=lgx與y=-x+3的圖象.
它們的交點橫坐標x
0.
當x=2時,lgx=lg2,3-x=1.
∵lg2<1=lg10,
∴x
0>2,
從而判定x
0∈(2,3).
故選B.
點評:本題主要考查了函數的零點與方程根的關系,考查通過構造函數用數形結合法求方程lgx+x-3=0解所在的區間.數形結合,要在結合方面下功夫.不僅要通過圖象直觀估計,而且還要計算x0的鄰近兩個函數值,通過比較其大小進行判斷.

 解:lgx+x-3=0可化為:lgx=-x+3,
解:lgx+x-3=0可化為:lgx=-x+3,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案