Question

【題目】已知Sn為等比數列{an}的前n項和且S4=S3+3a3 ， a2=9．
（1）求數列{an}的通項公式
（2）設bn=（2n﹣1）an ， 求數列{bn}的前n項和Tn ．

Answer 1

【答案】
（1）解：設等比數列{an}的公比為q，

S4=S3+3a3，a2=9，可得

a4=S4﹣S3=3a3，即q= =3，

a1q=9，可得a1=3，

則數列{an}的通項公式為an=a1qn﹣1=3n；

（2）解：bn=（2n﹣1）an=（2n﹣1）3n；

則前n項和Tn=131+332+…+（2n﹣1）3n；

3Tn=132+333+…+（2n﹣1）3n+1；

兩式相減可得，﹣2Tn=3+2（32+33+…+3n）﹣（2n﹣1）3n+1

=3+2 ﹣（2n﹣1）3n+1；

化簡可得Tn=3+（n﹣1）3n+1．

【解析】（1）設等比數列{an}的公比為q，運用等比數列的通項公式可得首項和公比，即可得到所求通項公式；（2）求得bn=（2n﹣1）an=（2n﹣1）3n；運用數列的求和方法：錯位相減法，結合等比數列的求和公式，化簡整理即可得到所求和．
【考點精析】本題主要考查了數列的前n項和和數列的通項公式的相關知識點，需要掌握數列{an}的前n項和sn與通項an的關系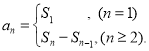；如果數列an的第n項與n之間的關系可以用一個公式表示，那么這個公式就叫這個數列的通項公式才能正確解答此題．