
【題目】已知數列![]() 的首項為1,且
的首項為1,且![]() ,數列
,數列![]() 滿足
滿足![]() ,
,![]() ,對任意
,對任意![]() ,都有
,都有![]() .
.
(1)求數列![]() 、
、![]() 的通項公式;
的通項公式;
(2)令![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() .若對任意的
.若對任意的![]() ,不等式
,不等式![]() 恒成立,試求實數
恒成立,試求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
試題(1)由![]() ,得
,得![]() ,又
,又![]() ,兩式相減得
,兩式相減得![]() ,整理得
,整理得![]() ,即
,即![]() ,又因為
,又因為![]() ,
,![]() ,
,
利用累積法得![]() ,
,
從而可求出數學![]() 的通項公式為
的通項公式為![]() ;
;
在數列![]() 中,由
中,由![]() ,得
,得![]() ,且
,且![]() ,
,
所以數學![]() 是以首項為
是以首項為![]() ,公比為
,公比為![]() 的等比數列,從而數列
的等比數列,從而數列![]() 的通項公式為
的通項公式為![]() .
.
(2)由題意得![]() ,
,
![]() ,
,
兩式相減得![]()
![]() ,
,
由等比數列前![]() 項和公式可求得
項和公式可求得![]() ,
,
由不等式![]() 恒成立,得
恒成立,得![]() 恒成立,
恒成立,
即![]() (
(![]() )恒成立,
)恒成立,
構造函數![]() (
(![]() ),
),
當![]() 時,
時,![]() 恒成立,則
恒成立,則![]() 不滿足條件;
不滿足條件;
當![]() 時,由二次函數性質知不恒成立;
時,由二次函數性質知不恒成立;
當![]() 時,
時,![]() 恒成立,則
恒成立,則![]() 滿足條件.
滿足條件.
綜上所述,實數![]() 的取值范圍是
的取值范圍是![]() .
.
試題解析:(1)∵![]() ,∴
,∴![]() (
(![]() ),兩式相減得,
),兩式相減得,![]() ,
,
∴![]() ,即
,即![]() (
(![]() ),又因為
),又因為![]() ,
,![]() ,從而
,從而![]()
∴![]() (
(![]() ),
),
故數列![]() 的通項公式
的通項公式![]() (
(![]() ).
).
在數列![]() 中,由
中,由![]() ,知數列
,知數列![]() 是等比數列,首項、公比均為
是等比數列,首項、公比均為![]() ,
,
∴數列![]() 的通項公式
的通項公式![]() .
.
(2)∴![]() ①
①
∴![]() ②
②
由①-②,得![]()
![]() ,
,
∴![]() ,
,
不等式![]() 即為
即為![]() ,
,
即![]() (
(![]() )恒成立.
)恒成立.
方法一、設![]() (
(![]() ),
),
當![]() 時,
時,![]() 恒成立,則
恒成立,則![]() 不滿足條件;
不滿足條件;
當![]() 時,由二次函數性質知不恒成立;
時,由二次函數性質知不恒成立;
當![]() 時,
時,![]() 恒成立,則
恒成立,則![]() 滿足條件.
滿足條件.
綜上所述,實數λ的取值范圍是![]() .
.
方法二、也即![]() (
(![]() )恒成立,
)恒成立,
令![]() .則
.則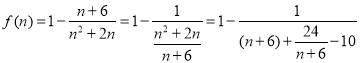 ,
,
由![]() ,
,![]() 單調遞增且大于0,∴
單調遞增且大于0,∴![]() 單調遞增∴
單調遞增∴![]()
∴實數λ的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】已知f(x)是定義域為(0,+∞)的單調函數,若對任意的x∈(0,+∞),都有 ![]() ,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在區間(0,3]上有兩解,則實數a的取值范圍是( )
,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在區間(0,3]上有兩解,則實數a的取值范圍是( )
A.0<a≤5
B.a<5
C.0<a<5
D.a≥5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知橢圓 ![]() (a>b>0)的離心率為
(a>b>0)的離心率為 ![]() ,焦點到相應準線的距離為1.
,焦點到相應準線的距離為1. 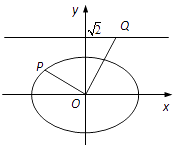
(1)求橢圓的標準方程;
(2)若P為橢圓上的一點,過點O作OP的垂線交直線 ![]() 于點Q,求
于點Q,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩個同學分別拋擲一枚質地均勻的骰子.
(1)求他們拋擲的骰子向上的點數之和是4的倍數的概率;
(2)求甲拋擲的骰子向上的點數不大于乙拋擲的骰子向上的點數的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海南沿海某次超強臺風過后,當地人民積極恢復生產,焊接工王師傅每天都很忙碌.一天他遇到了一個難題:如圖所示,有一塊扇形鋼板,半徑為![]() 米,圓心角
米,圓心角![]() ,施工要求按圖中所畫的那樣,在鋼板
,施工要求按圖中所畫的那樣,在鋼板![]() 上裁下一塊平行四邊形鋼板
上裁下一塊平行四邊形鋼板![]() ,要求使裁下的鋼板面積最大.請你幫助王師傅解決此問題.連接
,要求使裁下的鋼板面積最大.請你幫助王師傅解決此問題.連接![]() ,設
,設![]() ,過
,過![]() 作
作![]() ,垂足為
,垂足為![]() .
.

(1)求線段![]() 的長度(用
的長度(用![]() 來表示);
來表示);
(2)求平行四邊形![]() 面積的表達式(用
面積的表達式(用![]() 來表示);
來表示);
(3)為使平行四邊形![]() 面積最大,
面積最大,![]() 等于何值?最大面積是多少?
等于何值?最大面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱![]() (側棱垂直于底面)中,
(側棱垂直于底面)中,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中點,在線段
的中點,在線段![]() 上是否存在一點
上是否存在一點![]() 使
使![]() 平面
平面![]() ?若存在,請確定點
?若存在,請確定點![]() 的位置;若不存在,也請說明理由.
的位置;若不存在,也請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九大指出中國的電動汽車革命早已展開,通過以新能源汽車替代汽/柴油車,中國正在大力實施一項將重塑全球汽車行業的計劃.![]() 年某企業計劃引進新能源汽車生產設備,通過市場分析,全年需投入固定成本
年某企業計劃引進新能源汽車生產設備,通過市場分析,全年需投入固定成本![]() 萬元,每生產
萬元,每生產![]() (百輛),需另投入成本
(百輛),需另投入成本![]() 萬元,且
萬元,且 .由市場調研知,每輛車售價
.由市場調研知,每輛車售價![]() 萬元,且全年內生產的車輛當年能全部銷售完.
萬元,且全年內生產的車輛當年能全部銷售完.
(1)求出2018年的利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (百輛)的函數關系式;(利潤=銷售額-成本)
(百輛)的函數關系式;(利潤=銷售額-成本)
(2)2018年產量為多少百輛時,企業所獲利潤最大?并求出最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com