
(本題滿分15分)
已知函數(shù)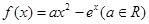 ,
,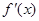 是
是 的導(dǎo)函數(shù)(
的導(dǎo)函數(shù)( 為自然對數(shù)的底數(shù))
為自然對數(shù)的底數(shù))
(Ⅰ)解關(guān)于 的不等式:
的不等式: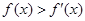 ;
;
(Ⅱ)若 有兩個極值點
有兩個極值點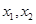 ,求實數(shù)
,求實數(shù)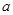 的取值范圍.
的取值范圍.
(Ⅰ)當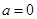 時,無解;當
時,無解;當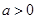 時,解集為
時,解集為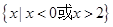 ;當
;當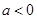 時,解集為
時,解集為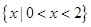 ;(Ⅱ)
;(Ⅱ)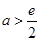 。
。
【解析】
試題分析:解:(Ⅰ)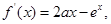 …………………………2分
…………………………2分
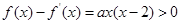 …………………………4分
…………………………4分
當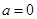 時,無解;
…………………………5分
時,無解;
…………………………5分
當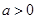 時,解集為
時,解集為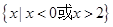 ;
…………………………6分
;
…………………………6分
當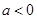 時,解集為
時,解集為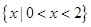 …………………………7分
…………………………7分
(Ⅱ)方法一:若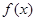 有兩個極值點
有兩個極值點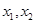 ,則
,則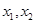 是方程
是方程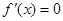 的兩個根
的兩個根
 ,顯然
,顯然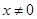 ,得:
,得: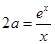 ……………………………9分
……………………………9分
令 ,
…………………………11分
,
…………………………11分
若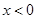 時,
時, 單調(diào)遞減且
單調(diào)遞減且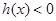 ,
…………………………12分
,
…………………………12分
若 時,當
時,當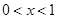 時,
時,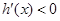 ,
, 在
在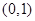 上遞減,
上遞減,
當 時,
時,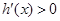 ,
, 在
在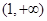 上遞增,
上遞增, ……14分
……14分
要使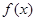 有兩個極值點,需滿足
有兩個極值點,需滿足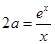 在
在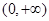 上有兩個不同解,
上有兩個不同解,
得: ,即:
,即: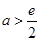 ……………………15分
……………………15分
法二:設(shè)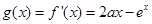 ,
,
則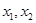 是方程
是方程 的兩個根,則
的兩個根,則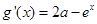 ,
…………………………9分
,
…………………………9分
若 時,
時, 恒成立,
恒成立,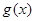 單調(diào)遞減,方程
單調(diào)遞減,方程 不可能有兩個根……11分
不可能有兩個根……11分
若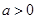 時,由
時,由 ,得
,得 ,
,
當 時,
時,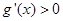 ,
,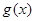 單調(diào)遞增,
單調(diào)遞增,
當 時,
時, 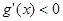
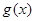 單調(diào)遞減
…………………………13分
單調(diào)遞減
…………………………13分
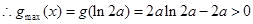 ,得
,得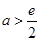 …………………………15分
…………………………15分
考點:一元二次含參不等式的解法。利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性和極值。
點評:(1)解一元二次含參不等式的主要思想是分類討論,常討論的有二次項系數(shù)、兩根的大小和判別式?;(2)第二問方法一的關(guān)鍵是把問題轉(zhuǎn)化為“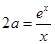 有兩個不同解”,根據(jù)構(gòu)造函數(shù)來求。
有兩個不同解”,根據(jù)構(gòu)造函數(shù)來求。


 怎樣學(xué)好牛津英語系列答案
怎樣學(xué)好牛津英語系列答案 導(dǎo)學(xué)教程高中新課標系列答案
導(dǎo)學(xué)教程高中新課標系列答案科目:高中數(shù)學(xué) 來源:2010-2011年江蘇省如皋市五校高二下學(xué)期期中考試理科數(shù)學(xué) 題型:解答題
((本題滿分15分)
某有獎銷售將商品的售價提高120元后允許顧客有3次抽獎的機會,每次抽獎的方法是在已經(jīng)設(shè)置并打開了程序的電腦上按“Enter”鍵,電腦將隨機產(chǎn)生一個 1~6的整數(shù)數(shù)作為號碼,若該號碼是3的倍數(shù)則顧客獲獎,每次中獎的獎金為100元,運用所學(xué)的知識說明這樣的活動對商家是否有利。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年浙江省招生適應(yīng)性考試文科數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分15分)設(shè)函數(shù) .
.
(Ⅰ)若函數(shù) 在
在 上單調(diào)遞增,在
上單調(diào)遞增,在 上單調(diào)遞減,求實數(shù)
上單調(diào)遞減,求實數(shù) 的最大值;
的最大值;
(Ⅱ)若 對任意的
對任意的 ,
, 都成立,求實數(shù)
都成立,求實數(shù) 的取值范圍.
的取值范圍.
注: 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年浙江省溫州市十校聯(lián)合體高三上學(xué)期期初摸底文科數(shù)學(xué) 題型:解答題
(本題滿分15分)已知直線 與曲線
與曲線 相切
相切
1)求b的值;
2)若方程 在
在 上恰有兩個不等的實數(shù)根
上恰有兩個不等的實數(shù)根 ,求
,求
①m的取值范圍;
②比較 的大小
的大小
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年浙江省溫州市十校聯(lián)合體高三上學(xué)期期中考試文科數(shù)學(xué) 題型:解答題
(本題滿分15分)已知拋物線 :
: (
( ),焦點為
),焦點為 ,直線
,直線 交拋物線
交拋物線 于
于 、
、 兩點,
兩點, 是線段
是線段 的中點,
的中點,
過 作
作 軸的垂線交拋物線
軸的垂線交拋物線 于點
于點 ,
,
(1)若拋物線 上有一點
上有一點 到焦點
到焦點 的距離為
的距離為 ,求此時
,求此時 的值;
的值;
(2)是否存在實數(shù) ,使
,使 是以
是以 為直角頂點的直角三角形?若存在,求出
為直角頂點的直角三角形?若存在,求出 的值;若不存在,說明理由。
的值;若不存在,說明理由。

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年浙江省六校高三第一次聯(lián)考文科數(shù)學(xué) 題型:解答題
(本題滿分15分)
已知函數(shù)
(1)求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)設(shè) ,若
,若 在
在 上不單調(diào)且僅在
上不單調(diào)且僅在 處取得最大值,求
處取得最大值,求 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com