解:(1)集合M={0,2,4}具有性質P,N={1,2,3}不具有性質P.
∵集合M={0,2,4}中,aj+ai與aj-ai(1≤i≤j≤2)兩數中都是該數列中的項,4-2是該數列中的項,∴集合M={0,2,4}具有性質P;
N={1,2,3}中,3在此集合中,則由題意得3+3和3-3至少一個一定在,而3+3=6不在,所以3-3=0一定是這個集合的元素,而此集合沒有0,故不具有性質P;
(2)若數列A具有性質P,則an+an=2an與an-an=0兩數中至少有一個是該數列中的一項,
∵0≤a1<a2<…<an,n≥3,而2an不是該數列中的項,∴0是該數列中的項,
∴a1=0;
n=3時,∵數列a1,a2,a3具有性質P,0≤a1<a2<a3
∴a2+a3與a3-a2至少有一個是該數列中的一項,
∵a1=0,a2+a3不是該數列的項,∴a3-a2=a2,∴a1+a3=2a2,數列{an}一定成等差數列;
n=4時,∵數列a1,a2,a3,a4具有性質P,0≤a1<a2<a3<a4,
∴a3+a4與a4-a3至少有一個是該數列中的一項,
∵a3+a4不是該數列的項,∴a4-a3=a2,或a4-a3=a3,
若a4-a3=a2,則數列{an}一定成等差數列;若a4-a3=a3,則數列{an}不一定成等差數列;
n=5時,∵數列a1,a2,a3,a4,a5有性質P,0≤a1<a2<a3<a4<a5,
∴a4+a5與a5-a4至少有一個是該數列中的一項,
∵a4+a5不是該數列的項,∴a5-a4=a2,或a5-a4=a3,或a5-a4=a4,
若a5-a4=a4,a4-a3=a2,則數列{an}一定成等差數列;若a5-a4=a2,或a5-a4=a3,則數列{an}不一定成等差數列.
分析:(1)利用新定義,可以判斷集合M={0,2,4}具有性質P,N={1,2,3}不具有性質P;
(2)確定a1=0,再利用新定義,即可判斷具有性質P的集合A中的數列{an}是否一定成等差數列.
點評:本題考查數列的綜合應用,考查學生的應用知識分析、解決問題的能力,屬于難題.

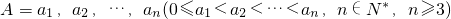 具有性質P:對任意i,j(1≤i≤j≤n),ai+aj與aj-ai至少一個屬于A.
具有性質P:對任意i,j(1≤i≤j≤n),ai+aj與aj-ai至少一個屬于A.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案