
已知關于x的方程:x2-(6+i)x+9+ai=0(a∈R)有實數根b.
(1)求實數a,b的值.
(2)若復數滿足| -a-bi|-2|z|=0,求z為何值時,|z|有最小值,并求出|z|的最小值.
-a-bi|-2|z|=0,求z為何值時,|z|有最小值,并求出|z|的最小值.
(1)a=b=3 (1) 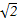
【解析】【思路點撥】(1)把b代入方程,根據復數的實部、虛部等于0解題即可.
(2)設z=s+ti(s,t∈R),根據所給條件可得s,t間的關系,進而得到復數z對應的軌跡,根據軌跡解決|z|的最值問題.
【解析】
(1)∵b是方程x2-(6+i)x+9+ai=0(a∈R)的實根,
∴(b2-6b+9)+(a-b)i=0,
∴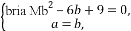 解得a=b=3.
解得a=b=3.
(2)設z=s+ti(s,t∈R),其對應點為Z(s,t),
由|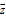 -3-3i|=2|z|,
-3-3i|=2|z|,
得(s-3)2+(t+3)2=4(s2+t2),
即(s+1)2+(t-1)2=8,
∴Z點的軌跡是以O1(-1,1)為圓心,2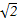 為半徑的圓,如圖所示,
為半徑的圓,如圖所示,
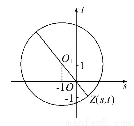
當Z點在OO1的連線上時,|z|有最大值或最小值.
∵|OO1|=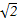 ,半徑r=2
,半徑r=2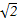 ,
,
∴當z=1-i時,|z|有最小值且|z|min=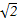 .
.


科目:高中數學 來源:2014年高考數學全程總復習課時提升作業二十四第三章第八節練習卷(解析版) 題型:選擇題
某人在C點測得某塔在南偏西80°,塔頂仰角為45°,此人沿南偏東40°方向前進10米到D,測得塔頂A的仰角為30°,則塔高為( )
(A)15米 (B)5米
(C)10米 (D)12米
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業二十五第四章第一節練習卷(解析版) 題型:填空題
已知△ABC中,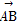 =a,
=a,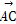 =b,對于平面ABC上任意一點O,動點P滿足
=b,對于平面ABC上任意一點O,動點P滿足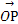 =
=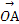 +λa+λb,則動點P的軌跡所過的定點為 .
+λa+λb,則動點P的軌跡所過的定點為 .
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業二十二第三章第六節練習卷(解析版) 題型:解答題
設函數f(x)=2cos2x+2 sinxcosx-1(x∈R).
sinxcosx-1(x∈R).
(1)化簡函數f(x)的表達式,并求函數f(x)的最小正周期.
(2)若x∈[0,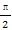 ],求函數f(x)的最大值與最小值.
],求函數f(x)的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業二十二第三章第六節練習卷(解析版) 題型:選擇題
已知函數f(x)=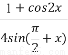 -asin
-asin cos(π-
cos(π- )的最大值為2,則常數a的值為( )
)的最大值為2,則常數a的值為( )
(A)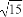 (B)-
(B)-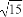
(C)±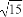 (D)±
(D)±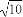
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業二十九第四章第五節練習卷(解析版) 題型:選擇題
若sin2θ-1+i(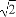 cosθ+1)是純虛數,則θ的值為( )
cosθ+1)是純虛數,則θ的值為( )
(A)2kπ- ,k∈Z(B)2kπ+
,k∈Z(B)2kπ+ ,k∈Z
,k∈Z
(C)2kπ± ,k∈Z(D)
,k∈Z(D) π+
π+ ,k∈Z
,k∈Z
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業二十九第四章第五節練習卷(解析版) 題型:選擇題
已知復數z=1+i,則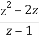 等于( )
等于( )
(A)2i(B)-2i(C)2(D)-2
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業二十七第四章第三節練習卷(解析版) 題型:解答題
在平面直角坐標系中,已知向量a=(-1,2),又點A(8,0),B(n,t),C(ksinθ,t)(0≤θ≤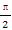 ).
).
(1)若 ⊥a,且|
⊥a,且| |=
|=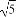 |
|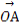 |(O為坐標原點),求向量
|(O為坐標原點),求向量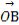 .
.
(2)若向量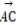 與向量a共線,當k>4,且tsinθ取最大值4時,求
與向量a共線,當k>4,且tsinθ取最大值4時,求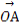 ·
·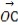 .
.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業三十第五章第一節練習卷(解析版) 題型:選擇題
已知數列{an}的前n項和Sn=n2-9n,第k項滿足5<ak<8,則k等于( )
(A)9(B)8(C)7(D)6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com