
(本題12分)某研究機構對高三學生的記憶力x和判斷力y進行統計分析,得下表數據
|
x |
6 |
8 |
10 |
12 |
|
y |
2 |
3 |
5 |
6 |
(1)請畫出上表數據的散點圖;(2)請根據上表提供的數據,求出y關于x的線性回歸方程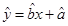 ;(3)試根據(2)求出的線性回歸方程,預測記憶力為9的同學的判斷力.(相關公式:
;(3)試根據(2)求出的線性回歸方程,預測記憶力為9的同學的判斷力.(相關公式: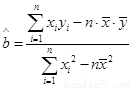 ,
,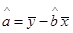 )
)
(1)見解析;(2)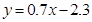 ;(3)記憶力為9的同學的判斷力約為4。
;(3)記憶力為9的同學的判斷力約為4。
【解析】
試題分析:(Ⅰ)如右圖
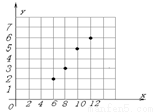 ┄┄┄┄3分
┄┄┄┄3分
(Ⅱ)解: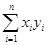 =6
=6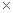 2+8
2+8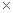 3+10
3+10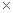 5+12
5+12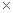 6=158,
6=158,
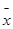 =
=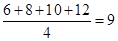 ,
,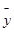 =
=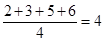 ,
,
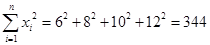 ,
, 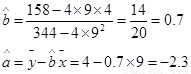
故線性回歸方程為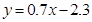 .
┄┄┄┄┄┄┄┄10分
.
┄┄┄┄┄┄┄┄10分
(Ⅲ)解:由回歸直線方程預測,記憶力為9的同學的判斷力約為4. ┄┄┄┄┄12分
考點:散點圖;線性回歸直線方程;回歸分析。
點評:本題考查線性回歸方程的求法和應用,解題的關鍵是利用最小二乘法做出線性回歸方程的系數,注意不要出現計算錯誤。屬于基礎題型。在由回歸直線方程預測,我們要注意說法,比如此題,正確說法是:記憶力為9的同學的判斷力約為4,但要是說成由回歸直線方程預測,記憶力為9的同學的判斷力為4,去掉了“約”字,就錯誤。


科目:高中數學 來源:2012-2013學年黑龍江省高二上學期期末考試理科數學試卷(解析版) 題型:解答題
(本題12分)為了研究化肥對小麥產量的影響,某科學家將一片土地劃分成200個 的小塊,并在100個小塊上施用新化肥,留下100個條件大體相當的小塊不施用新化肥.下表1和表2分別是施用新化肥和不施用新化肥的小麥產量頻數分布表(小麥產量單位:kg)
的小塊,并在100個小塊上施用新化肥,留下100個條件大體相當的小塊不施用新化肥.下表1和表2分別是施用新化肥和不施用新化肥的小麥產量頻數分布表(小麥產量單位:kg)
表1:施用新化肥小麥產量頻數分布表
|
小麥產量 |
|
|
|
|
|
|
頻數 |
10 |
35 |
40 |
10 |
5 |
表2:不施用新化肥小麥產量頻數分布表
|
小麥產量 |
|
|
|
|
|
頻數 |
15 |
50 |
30 |
5 |
(10) 完成下面頻率分布直方圖;

(2)統計方法中,同一組數據常用該組區間的中點值作為代表,據此估計施用化肥和不施用化肥的一小塊土地的小麥平均產量;
(3)完成下面2×2列聯表,并回答能否有99.5%的把握認為“施用新化肥和不施用新化肥的小麥產量有差異”
表3:
|
|
小麥產量小于20kg |
小麥產量不小于20kg |
合計 |
|
施用新化肥 |
|
|
|
|
不施用新化肥 |
|
|
|
|
合計 |
|
|
|
附:
|
|
0.050 |
0.010 |
0.005 |
0.001 |
|
|
3.841 |
6.635 |
7.879 |
10.828 |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年湖北省武漢市武昌區高三5月調研考試文科數學試卷(解析版) 題型:解答題
(本題滿分12分)
某科研所研究人員都具有本科和研究生兩類學歷,年齡段和學歷如下表,從該科研所任選一名研究人員,是本科生概率是 ,是35歲以下的研究生概率是
,是35歲以下的研究生概率是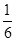 .
.
|
|
本科(單位:名) |
研究生(單位:名) |
|
35歲以下 |
3 |
y |
|
35—50歲 |
3 |
2 |
|
50歲以上 |
x |
0 |
(Ⅰ)求出表格中的x和y的值;
(Ⅱ)設“從數學教研組任選兩名教師,本科一名,研究生一名,50
歲以上本科生和35歲以下的研究生不全選中” 的事件為A,求事件A概率 .
.
查看答案和解析>>
科目:高中數學 來源:安徽省2010屆高三第三次模擬考試數學(文)試卷 題型:解答題
(本題滿分12分)某學校課題組為了研究學生的數學成績與物理成績之間的關系,隨機抽取高二年級20名學生某次考試成績(滿分100分)如下表所示:
|
序號 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
數學 成績 |
95 |
75 |
80 |
94 |
92 |
65 |
67 |
84 |
98 |
71 |
67 |
93 |
64 |
78 |
77 |
90 |
57 |
83 |
72 |
83 |
|
物理 成績 |
90 |
63 |
72 |
87 |
91 |
71 |
58 |
82 |
93 |
81 |
77 |
82 |
48 |
85 |
69 |
91 |
61 |
84 |
78 |
86 |
若單科成績85分以上(含85分),則該科成績為優秀.
(1)根據上表完成下面的2×2列聯表(單位:人):
|
|
數學成績優秀 |
數學成績不優秀 |
合 計 |
|
物理成績優秀 |
|
|
|
|
物理成績不優秀 |
|
|
|
|
合 計 |
|
|
20 |
(2)根據題(1)中表格的數據計算,有多大的把握,認為學生的數學成績與物理成績之間有關系?
(3)若從這20個人中抽出1人來了解有關情況,求抽到的學生數學成績與物理成績至少有一門不優秀的概率.
參考數據及公式:
①隨機變量 ,其中
,其中 為樣本容量;
為樣本容量;
②獨立檢驗隨機變量 的臨界值參考表:
的臨界值參考表:
|
|
0.010 |
0.005 |
0.001 |
|
|
6.635 |
7.879 |
10.828 |
查看答案和解析>>
科目:高中數學 來源:2010-2011年安徽省高二第二學期期中考試數學試卷 題型:解答題
(本題12分)
某學校高三年級有學生1000名,經調查研究,其中750名同學經常參加體育鍛煉(稱為A類同學),另外250名同學不經常參加體育鍛煉(稱為B類同學),現用分層抽樣方法(按 A類、B類分二層)從該年級的學生中共抽查100名同學,如果以身高達165cm作為達標的標準,對抽取的100名學生,得到以下列聯表:
體育鍛煉與身高達標2×2列聯表
|
|
身高達標 |
身高不達標 |
總計 |
|
積極參加 體育鍛煉 |
40 |
|
|
|
不積極參加 體育鍛煉 |
|
15 |
|
|
總計 |
|
|
100 |
(1)完成上表;
(2)請問有多大的把握認為體育鍛煉與身高達標有關系(K2值精確到0.01)?
參考公式:K2=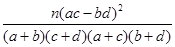 ,參考數據:
,參考數據:
|
P(K2≥k0) |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
|
K0 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com