分析:第①個命題說明回歸直線通過樣本中心點.
②:由冪函數的概念判斷出m
2-m-1等于1;列出等式求出m,再根據象關于y軸對稱驗證其指數為偶數.再判斷其單調性;
③:先利用導數求出函數
f(x)=ax3-bx2+ax+π在R上有兩個相異極值點的充要條件,得出關于a,b的約束條件,在a-o-b坐標系中畫出可行域,再利用幾何概型求出兩者的面積比即可.
④:特稱命題“?x∈[1,2],x
2-1≥0”的否定是:把?改為?,其它條件不變,然后否定結論,變為一個特稱命題.即“?x∈[1,2],x
2-1<0”.
解答:解:對于①,已知n個散點A
i(x
i,y
i),(i=1,2,3,…,n)的線性回歸方程為
=bx+a,若
a=-b,(其中
=| n |
 |
| i=1 |
xi,
=| n |
 |
| i=1 |
yi),則此回歸直線必經過點(
,),這說明回歸直線一定經過樣本中心點,故正確.
對于②:∵冪函數f(x)=(m
2-m-1)x
1-m∴m
2-m-1=1⇒m=-1或m=2
當m=2時,冪函數f(x)=(m
2-m-1)x
1-m=x
-1,
它不在R上是減函數,故錯;
③:易得f′(x)=ax
2-2bx+a,
對于函數
f(x)=ax3-bx2+ax+π在R上有兩個相異極值點的充要條件:
是a≠0且其導函數的判別式大于0,即a≠0且4b
2-4a
2>0,
又若a,b在區間[0,1]上取值,則b>a,
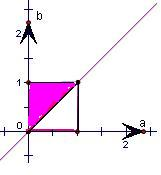
點(a,b)滿足的區域如圖中陰影部分所示,
其中正方形區域的面積為1,陰影部分的面積為
,
但反之不能成立,因為當a,b在區間[1,2]上取值時,也得到有兩相異極值點的概率為
”.故錯.
對于④,全稱命題“?x∈[1,2],x
2-1≥0”的否定是特稱命題:“?x∈[1,2],x
2-1<0”.故正確.
故選C.
點評:本小題主要考查函數單調性的應用、命題的否定、線性回歸方程、幾何概型等基礎知識,考查運算求解能力,考查轉化思想.屬于基礎題.






 ③:易得f′(x)=ax2-2bx+a,
③:易得f′(x)=ax2-2bx+a,
