
【題目】下列說法正確的個數(shù)為( )
①命題“![]() 中,若
中,若![]() ,則
,則![]() ”的逆命題是真命題
”的逆命題是真命題
②若命題![]() ,則
,則![]()
③“命題![]() 為真命題”是“命題
為真命題”是“命題![]() 為假命題”的充要條件
為假命題”的充要條件
④設(shè)![]() 均為非零向量,則“
均為非零向量,則“![]() ”是“
”是“![]() 與
與![]() 的夾角為銳角”的必要不充分條件
的夾角為銳角”的必要不充分條件
A.1B.2C.3D.4
【答案】C
【解析】
①由正弦定理判斷.②根據(jù)全稱命題的否定是特稱命題判斷.③根據(jù)“命題![]() 為真命題”則p,q都為真命題判斷.④根據(jù)
為真命題”則p,q都為真命題判斷.④根據(jù)![]() ,當(dāng)
,當(dāng)![]() 時判斷.
時判斷.
①命題“![]() 中,若
中,若![]() ,則
,則![]() ”的逆命題是:命題“
”的逆命題是:命題“![]() 中,
中,
若![]() ,則
,則![]() ”,若
”,若 ![]() ,由正弦定理得
,由正弦定理得![]() ,所以
,所以![]() ,是真命題,故正確.
,是真命題,故正確.
②因?yàn)槿Q命題的否定是特稱命題,故正確.
③因?yàn)?/span>“命題![]() 為真命題”,則p,q都為真命題,則“命題
為真命題”,則p,q都為真命題,則“命題![]() 為假命題”,故充分,因?yàn)?/span>“命題
為假命題”,故充分,因?yàn)?/span>“命題![]() 為假命題”,說明
為假命題”,說明![]() 為真命題,但
為真命題,但![]() 的真假不確定,則
的真假不確定,則![]() 的真假不確定,故不必要,故錯誤.
的真假不確定,故不必要,故錯誤.
④因?yàn)?/span>![]() ,當(dāng)
,當(dāng)![]() 與
與![]() 的夾角為銳角時,
的夾角為銳角時,![]() ,故必要,當(dāng)
,故必要,當(dāng)![]() 時,
時,![]() 滿足條件,但不是銳角,故不充分,故必要不充分,故正確.
滿足條件,但不是銳角,故不充分,故必要不充分,故正確.
故選:C


 計(jì)算高手系列答案
計(jì)算高手系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】數(shù)學(xué)名著《算學(xué)啟蒙》中有關(guān)于“松竹并生”的問題:松長四尺,竹長兩尺,松日自半,竹日自倍,松竹何日而長等.如圖,是源于其思想的一個程序框圖.若輸入的![]() 分別為8、2,則輸出的
分別為8、2,則輸出的![]() ( )
( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 在
在![]() 上的值域;
上的值域;
(2)若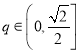 ,函數(shù)
,函數(shù)![]() 在
在![]() 上的最大值是
上的最大值是![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若不等式![]() 在
在![]() 上恒成立,求實(shí)數(shù)
上恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下圖是我國2010年至2016年生活垃圾無害化處理量(單位:億噸)的折線圖

注:年份代碼1~7分別對應(yīng)年份2010~2016
(1)由折線圖看出,可用線性回歸模型擬合y與t的關(guān)系,請求出相關(guān)系數(shù)r,并用相關(guān)系數(shù)的大小說明y與t相關(guān)性的強(qiáng)弱;
(2)建立y關(guān)于t的回歸方程(系數(shù)精確到0.01),預(yù)測2018年我國生活垃圾無害化處理量.
附注:
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
, ![]() .
.
參考公式:
相關(guān)系數(shù)
回歸方程![]() 中斜率和截距的最小二乘估計(jì)公式分別為:
中斜率和截距的最小二乘估計(jì)公式分別為:

![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
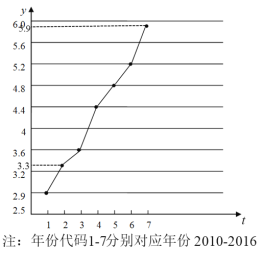
【題目】高血壓高血糖和高血脂統(tǒng)稱“三高”.如圖是西南某地區(qū)從2010年至2016年患“三高”人數(shù)y(單位:千人)的折線圖.
(1)由折線圖看出,可用線性回歸模型擬合![]() 與
與![]() 的關(guān)系,請求出相關(guān)系數(shù)(精確到0.01)并加以說明;
的關(guān)系,請求出相關(guān)系數(shù)(精確到0.01)并加以說明;
(2)建立![]() 關(guān)于
關(guān)于![]() 的回歸方程,預(yù)測2018年該地區(qū)患“三高”的人數(shù).
的回歸方程,預(yù)測2018年該地區(qū)患“三高”的人數(shù).
參考數(shù)據(jù):![]() ,
,![]() ,
,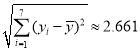 ,
,![]() .參考公式:相關(guān)系數(shù)
.參考公式:相關(guān)系數(shù)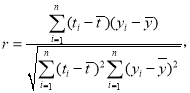 回歸方程
回歸方程![]() 中斜率和截距的最小二乘法估計(jì)公式分別為:
中斜率和截距的最小二乘法估計(jì)公式分別為:
![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
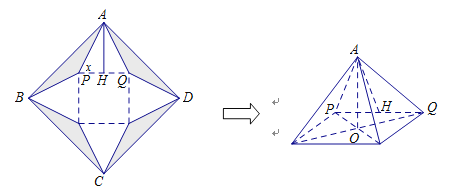
【題目】如圖:設(shè)一正方形紙片ABCD邊長為2分米,切去陰影部分所示的四個全等的等腰三角形,剩余為一個正方形和四個全等的等腰三角形,沿虛線折起,恰好能做成一個正四棱錐(粘接損耗不計(jì)),圖中![]() ,O為正四棱錐底面中心.
,O為正四棱錐底面中心.
(Ⅰ)若正四棱錐的棱長都相等,求這個正四棱錐的體積V;
(Ⅱ)設(shè)等腰三角形APQ的底角為x,試把正四棱錐的側(cè)面積S表示為x的函數(shù),并求S的范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() ,
,![]() ,
,![]() .
.
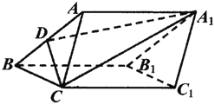
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com