日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

14．${∫}_{1}^{e}$（x+$\frac{1}{x}$）dx=（　　）
A．e2B．$\frac{{e}^{2}+1}{2}$C．$\frac{{e}^{2}-1}{2}$D．$\frac{{e}^{2}+3}{2}$

分析 根據(jù)定積分的計(jì)算法則計(jì)算即可．

解答 解：${∫}_{1}^{e}$（x+$\frac{1}{x}$）dx=（$\frac{1}{2}$x2+lnx）|${\;}_{1}^{e}$=（$\frac{1}{2}$e2+1）-（$\frac{1}{2}$+0）=$\frac{{e}^{2}+1}{2}$，
故選：B

點(diǎn)評 本題考查了定積分的計(jì)算，屬于基礎(chǔ)題．

練習(xí)冊系列答案
相關(guān)習(xí)題

科目：高中數(shù)學(xué) 來源： 題型：選擇題

2．設(shè)P={x|x＜4}，Q={x|x2＜4}，則（　　）
A．P⊆QB．Q⊆PC．P⊆∁RQD．Q⊆∁RP

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：選擇題

5．設(shè)函數(shù)f（x）=$\left\{\begin{array}{l}{（\frac{1}{3}）^{-x}-2，x≥0}\\{2lo{g}_{3}（-x），x＜0}\end{array}\right.$若f（m）＞1，則m的取值范圍是（　　）
A．（1，+∞）B．（-$\sqrt{3}$，1）C．（-∞，-$\sqrt{3}$）∪（1，+∞）D．（-∞，-$\sqrt{3}$）

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：選擇題

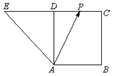2．如圖，四邊形ABCD是正方形，延長CD至E，使得DE=CD，若點(diǎn)P為CD的中點(diǎn)，且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$，則λ+μ=（　　）
A．3B．$\frac{5}{2}$C．2D．1

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

9．已知數(shù)列{an}滿足a1=1，an+1=2an+1（n∈N*）．若數(shù)列{bn}滿足：4${\;}^{{b_1}-1}}$•4${\;}^{{b_2}-1}}$•…4${\;}^{{b_n}-1}}$=（an+1）bn（n∈N*）．
（1）求數(shù)列{an}的通項(xiàng)公式；
（2）求證：{bn}是等差數(shù)列．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

19．設(shè)f（x）=ax2-a+$\frac{e}{{e}^{x}}$，g（x）=$\frac{1}{x}$+lnx．
（Ⅰ）設(shè)h（x）=f（x）-g（x）+$\frac{{e}^{x}-ex}{x{e}^{x}}$，討論y=h（x）的單調(diào)性；
（Ⅱ）證明：對任意a∈（-∞，$\frac{1}{2}$），?x∈（1，+∞），使f（x）＜g（x）成立．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

6．已知橢圓Γ的中心在原點(diǎn)，焦點(diǎn)在x軸，離心率為$\frac{{\sqrt{2}}}{2}$，且長軸長是短軸長的$\sqrt{2}$倍．
（1）求橢圓Γ的標(biāo)準(zhǔn)方程；
（2）設(shè)P（2，0）過橢圓Γ左焦點(diǎn)F的直線l交Γ于A，B兩點(diǎn)，若對滿足條件的任意直線l，不等式$\overrightarrow{PA}•\overrightarrow{PB}≤λ（{λ∈R}）$恒成立，求λ的最小值．

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：選擇題

3．設(shè)?x?表示不小于實(shí)數(shù)x的最小整數(shù)，如?2.6?=3，?-3.5?=-3．已知函數(shù)f（x）=?x?2-2?x?，若函數(shù)F（x）=f（x）-k（x-2）+2在（-1，4]上有2個零點(diǎn)，則k的取值范圍是（　　）
A．$[{-\frac{5}{2}，-1}）∪[2，5）$B．$（{-\frac{4}{3}，-1}]∪[5，10）$C．$[{-1，-\frac{2}{3}}）∪[5，10）$D．$[{-\frac{4}{3}，-1}]∪[5，10）$

查看答案和解析>>

科目：高中數(shù)學(xué) 來源： 題型：解答題

4．已知橢圓 C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左，右焦點(diǎn)分別是F1，F(xiàn)2，點(diǎn) D 在橢圓 C 上，DF1⊥F1F2，|F1F2|=4$\sqrt{3}$|DF|，△DFF的面積為$\frac{{\sqrt{3}}}{2}$．
（1）求橢圓C的方程；（2）圓x2+y2=b2的切線l交橢圓C于A，B兩點(diǎn)，求|AB|的最大值．

查看答案和解析>>

同步練習(xí)冊答案
主站蜘蛛池模板： 久久免费福利视频 | 亚洲天堂av网 | 午夜国产一区 | 天天干天天操天天 | 中文字幕不卡在线观看 | 精品国产三级 | 秋霞午夜鲁丝一区二区老狼 | 国产精品成人一区二区三区 | 国产亚洲欧美一区二区 | 欧美日韩在线免费观看 | 蜜臀久久99精品久久久久宅男 | 亚洲精品一区二区三区精华液 | 天天综合网站 | 国产精品123| 国产黄色免费看 | 亚洲精品在线观看视频 | 精品福利在线观看 | 天天爽夜夜操 | 中文字字幕在线中文 | 一本伊人 | 日韩视频免费观看 | 红桃av在线 | 日韩免费视频一区二区 | 欧美视频亚洲视频 | 免费一级全黄少妇性色生活片 | 中文字幕自拍 | 丰满少妇高潮无套内谢 | 日韩天堂在线 | 色婷婷基地 | 精品国产乱码久久久久久88av | 日韩和的一区二区 | av片在线观看 | 欧美日韩国产激情 | 日本黄色视 | 欧美日韩一| www.欧美日韩 | 国产精品久久久久永久免费看 | 亚洲欧洲在线观看 | 夜夜骑天天干 | 午夜精品久久 | 天天天天躁天天爱天天碰2018 |