
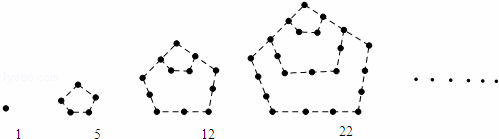
兩千多年前,古希臘畢達哥拉斯學派的數學家曾經在沙灘上研究數學問題,他們在沙灘上畫點或用小石子來表示數,按照點或小石子能排列的形狀對數進行分類,如圖中的實心點個數1,5,12,22,…,被稱為五角形數,其中第1個五角形數記作a1=1,第2個五角形數記作a2=5,第3個五角形數記作a3=12,第4個五角形數記作a4=22,…,若按此規律繼續下去,若an=145,則n= .
考點:
等比數列的通項公式;等差數列的通項公式.
專題:
等差數列與等比數列.
分析:
根據題目所給出的五角形數的前幾項,發現該數列的特點是,從第二項起,每一個數與前一個數的差構成了一個新的等差數列,寫出對應的n﹣1個等式,然后用累加的辦法求出該數列的通項公式,然后代入項求項數.
解答:
解:a2﹣a1=5﹣1=4,a3﹣a2=12﹣5=7,a4﹣a3=22﹣12=10,…,由此可知數列{an+1﹣an}構成以4為首項,以3為公差的等差數列.
所以an+1﹣an=4+3(n﹣1)=3n+1.
a2﹣a1=3×1+1
a3﹣a2=3×2+1
…
an﹣an﹣1=3(n﹣1)+1
累加得:an﹣a1=3(1+2+…+(n﹣1))+n﹣1
所以![]() =1+
=1+![]() +n﹣1=
+n﹣1=![]() .
.
由![]() ,解得:
,解得:![]() .
.
故答案為10.
點評:
本題考查了等差數列的通項公式,解答此題的關鍵是能夠由數列的前幾項分析出數列的特點,即從第二項起,每一個數與前一個數的差構成了一個新的等差數列,本題訓練了一種求數列通項的重要方法﹣﹣累加法.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
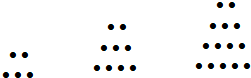 兩千多年前,古希臘畢達哥拉斯學派的數學家曾經在沙灘上研究數學問題.他們在沙灘上畫點或用小石子表示數,按照點或小石子能排列的形狀對數進行分類.如下圖中實心點的個數5,9,14,20,…為梯形數.根據圖形的構成,記此數列的第2013項為a2013,則a2013-5=( )
兩千多年前,古希臘畢達哥拉斯學派的數學家曾經在沙灘上研究數學問題.他們在沙灘上畫點或用小石子表示數,按照點或小石子能排列的形狀對數進行分類.如下圖中實心點的個數5,9,14,20,…為梯形數.根據圖形的構成,記此數列的第2013項為a2013,則a2013-5=( )查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源:2014屆廣東省高一6月月考數學試卷(解析版) 題型:填空題
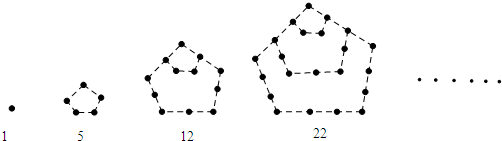
兩千多年前,古希臘畢達哥拉斯學派的數學家曾經在沙灘上研究數學問題,他們在沙灘上畫點或用小石子來表示數,按照點或小石子能排列的形狀對數進行分類,如圖1中的實心點個數1,5,12,22,…,被稱為五角形數,其中第1個五角形數記作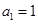 ,第2個五角形數記作
,第2個五角形數記作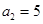 ,第3個五角形數記作
,第3個五角形數記作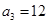 ,第4個五角形數記作
,第4個五角形數記作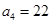 ,……,若按此規律繼續下去,則
,……,若按此規律繼續下去,則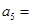 ,若
,若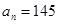 ,則
,則 .
.
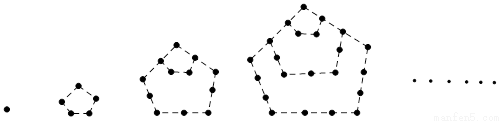
 1
5
12
22
1
5
12
22
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com