【題目】已知一圓的圓心
在直線
上，且該圓經過
和
兩點.
（1）求圓的標準方程；
（2）若斜率為
的直線
與圓相交于
，
兩點，試求
面積的最大值和此時直線的方程.
【答案】（1）
（2）最大值2，
或
.
【解析】
（1）方法一、求得
的垂直平分線方程與已知直線聯立，求得圓心，可得半徑，即可得到所求圓的方程；
方法二、設圓
的方程為
，將點代入可得
，
，
的方程組，解方程可得圓的方程；
（2）直線
與圓相交，設直線的方程為
，求得圓心到直線的距離和弦長，由三角形的面積公式，化為關于
的二次函數，求得最值，進而求得
，可得所求直線方程；
（1）方法一：
和
兩點的中垂線方程為：
，
圓心必在弦的中垂線上，聯立
得
，
半徑
，所以圓的標準方程為：.
方法二：設圓的標準方程為：
，
由題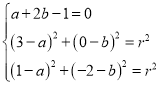得：
，解得：
所以圓的標準方程為：.
（2）設直線的方程為，圓心到直線的距離為
，
∴
，且
，
，
面積
，
當
，
時，
取得最大值2
此時
，解得：
或
所以，直線的方程為：或.
快樂5加2金卷系列答案科目：高中數學 來源： 題型：
【題目】如圖，已知AB是圓O的直徑，C是圓O上一點，AC=BC，且PA⊥平面ABC，E是AC的中點，F是PB的中點，PA=
，AB=2．求：
（Ⅰ）異面直線EF與BC所成的角；
（Ⅱ）點A到平面PBC的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】袋子中裝有除顏色外其他均相同的編號為a,b的兩個黑球和編號為c,d,e的三個紅球，從中任意摸出兩個球.
（1）求恰好摸出1個黑球和1個紅球的概率：
（2）求至少摸出1個黑球的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的兩個焦點分別為
，
，離心率為
，且橢圓四個頂點構成的菱形面積為
．
(1)求橢圓C的方程；
(2)若直線l ：y＝x＋m與橢圓C交于M，N兩點，以MN為底邊作等腰三角形，頂點為P(3，－2)，求m的值及△PMN的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下圖是某市11月1日至14日的空氣質量指數趨勢圖，空氣質量指數(AQI)小于100表示空氣質量優良，空氣質量指數大于200表示空氣重度污染，某人隨機選擇11月1日至11月12日中的某一天到達該市，并停留3天．
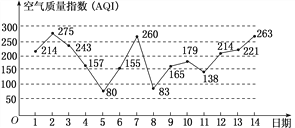
(1)求此人到達當日空氣重度污染的概率；
(2)設X是此人停留期間空氣重度污染的天數，求X的分布列與數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某興趣小組測量電視塔AE的高度H(單位m），如示意圖，垂直放置的標桿BC高度h=4m，仰角∠ABE=α，∠ADE=β
（1）該小組已經測得一組α、β的值，tanα=1.24,tanβ=1.20,,請據此算出H的值
（2）該小組分析若干測得的數據后，發現適當調整標桿到電視塔的距離d（單位m），使α與β之差較大，可以提高測量精確度，若電視塔實際高度為125m，問d為多少時，α-β最大
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學擬在高一下學期開設游泳選修課，為了了解高一學生喜歡游泳是否與性別有關，該學校對100名高一新生進行了問卷調查，得到如下列聯表：
喜歡游泳 | 不喜歡游泳 | 合計 | |
男生 | 10 | ||
女生 | 20 | ||
合計 |
已知在這100人中隨機抽取1人抽到喜歡游泳的學生的概率為
．
（1）請將上述列聯表補充完整；
（2）并判斷是否有99.9%的把握認為喜歡游泳與性別有關？并說明你的理由；
（3）已知在被調查的學生中有5名來自甲班，其中3名喜歡游泳，現從這5名學生中隨機抽取2人，求恰好有1人喜歡游泳的概率．
下面的臨界值表僅供參考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（參考公式：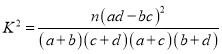
，其中
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
