
【題目】在極坐標系下,已知曲線C1:ρ=cosθ+sinθ和曲線C2:ρsin(θ-![]() )=
)=![]() .
.
(1)求曲線C1和曲線C2的直角坐標方程;
(2)當θ∈(0,π)時,求曲線C1和曲線C2公共點的一個極坐標.
【答案】(1)x2+y2-x-y=0,x-y+1=0;(2)![]() .
.
【解析】試題分析:(1)對![]() 的極坐標方程兩邊同乘
的極坐標方程兩邊同乘![]() ,將
,將![]() 的極坐標方程展開,再利用
的極坐標方程展開,再利用![]() 即可得曲線C1和曲線C2的直角坐標方程;(2)曲線C1和曲線C2的直角坐標方程聯立,求得曲線
即可得曲線C1和曲線C2的直角坐標方程;(2)曲線C1和曲線C2的直角坐標方程聯立,求得曲線![]() 與曲線
與曲線![]() 有公共點的一個直角坐標,再化為極坐標即可.
有公共點的一個直角坐標,再化為極坐標即可.
試題解析:(1)圓O:ρ=cos θ+sin θ,即ρ2=ρcos θ+ρsin θ,
曲線C1的直角坐標方程為:x2+y2=x+y,即x2+y2-x-y=0,
曲線C2:ρsin![]() =
=![]() ,即ρsin θ-ρcos θ=1,
,即ρsin θ-ρcos θ=1,
則曲線C2的直角坐標方程為:y-x=1,即x-y+1=0.
(2)由![]() 得
得![]()
則曲線C1和曲線C2公共點的一個極坐標為![]() .
.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)當a=2時,求(x)在x∈[1,e2]時的最值(參考數據:e2≈7.4);
(Ⅱ)若![]() ,有f(x)+g(x)≤0恒成立,求實數a的值;
,有f(x)+g(x)≤0恒成立,求實數a的值;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1: ![]() (t為參數)曲線C2:
(t為參數)曲線C2:![]() +y2=4.
+y2=4.
(1)在同一平面直角坐標系中,將曲線C2上的點按坐標變換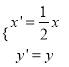 后得到曲線C′。求曲線C′的普通方程,并寫出它的參數方程;
后得到曲線C′。求曲線C′的普通方程,并寫出它的參數方程;
(2)若C1上的點P對應的參數為t=π/2,Q為C′上的動點,求PQ中點M到直線C3: ![]() (t為參數)的距離的最小值
(t為參數)的距離的最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() .
.
(1)求f(2)+f![]() ,f(3)+f
,f(3)+f![]() 的值;
的值;
(2)求證:f(x)+f![]() 是定值;
是定值;
(3)求f(2)+f![]() +f(3)+f
+f(3)+f![]() +…+
+…+![]() +f
+f![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為![]() .若直線
.若直線![]() 與圓C相交于不同的兩點P,Q.
與圓C相交于不同的兩點P,Q.
(Ⅰ)寫出圓C的直角坐標方程,并求圓心的坐標與半徑;
(Ⅱ)若弦長|PQ|=4,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了制定合理的節電方案,供電局對居民用電情況進行了調查,通過抽樣,獲得了某年200戶居民每戶的月均用電量(單位:度),將數據按照![]() ,
,![]() 分成9組,制成了如圖所示的頻率直方圖.
分成9組,制成了如圖所示的頻率直方圖.
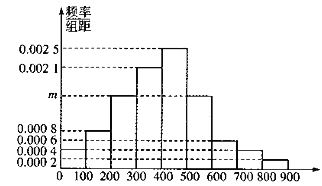
(1)求直方圖中![]() 的值并估計居民月均用電量的中位數;
的值并估計居民月均用電量的中位數;
(2)從樣本里月均用電量不低于700度的用戶中隨機抽取4戶,用![]() 表示月均用電量不低于800度的用戶數,求隨機變量
表示月均用電量不低于800度的用戶數,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩支籃球隊進行一局比賽,甲獲勝的概率為0.6,若采用三局兩勝制舉行一次比賽,現采用隨機模擬的方法估計乙獲勝的概率.
先利用計算器或計算機生成0到9之間取整數值的隨機數,用0,1,2,3,4,5表示甲獲勝;6,7,8,9表示乙獲勝,這樣能體現甲獲勝的概率為0.6.因為采用三局兩勝制,所以每3個隨機數作為一組.例如,產生30組隨機數.
034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959 774 246 762 428 114 572 042 533 237 322 707 360 751
據此估計乙獲勝的概率為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com