
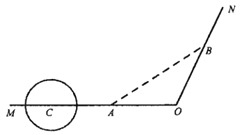
【題目】為解決城市的擁堵問題,某城市準備對現有的一條穿城公路MON進行分流,已知穿城公路MON自西向東到達城市中心![]() 后轉向
后轉向![]() 方向,已知∠MON=
方向,已知∠MON=![]() ,現準備修建一條城市高架道路L,L在MO上設一出入口A,在ON上設一出口B,假設高架道路L在AB部分為直線段,且要求市中心
,現準備修建一條城市高架道路L,L在MO上設一出入口A,在ON上設一出口B,假設高架道路L在AB部分為直線段,且要求市中心![]() 與AB的距離為10km.
與AB的距離為10km.
(1)求兩站點A,B之間的距離;
(2)公路MO段上距離市中心![]() 30km處有一古建筑群C,為保護古建筑群,設立一個以C為圓心,5km為半徑的圓形保護區.因考慮未來道路AB的擴建,則如何在古建筑群和市中心
30km處有一古建筑群C,為保護古建筑群,設立一個以C為圓心,5km為半徑的圓形保護區.因考慮未來道路AB的擴建,則如何在古建筑群和市中心![]() 之間設計出入口A,才能使高架道路及其延伸段不經過保護區?
之間設計出入口A,才能使高架道路及其延伸段不經過保護區?
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)過O作直線OE⊥AB于E,則OE=10,設∠EOA=![]() ,可求∠EOB=
,可求∠EOB=![]() ﹣
﹣![]() ,(
,(![]() ),可得AE=10tan
),可得AE=10tan![]() ,BE=10tan(
,BE=10tan(![]() ﹣
﹣![]() ),可求AB=
),可求AB=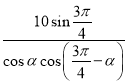 ,又
,又![]() ,結合
,結合![]() ,可得cos
,可得cos![]() ,可求兩出入口之間距離的最小值為20(
,可求兩出入口之間距離的最小值為20(![]() ).
).
(2)設切點為F,以![]() 為坐標原點,以
為坐標原點,以![]() 所在的直線為
所在的直線為![]() 軸,建立平面直角坐標系
軸,建立平面直角坐標系![]() ,設直線AB的方程為y=kx+t(k>0),可求t=20k,或t=60k,可求A(﹣20,0),此時OA=20,又由(1)可知當
,設直線AB的方程為y=kx+t(k>0),可求t=20k,或t=60k,可求A(﹣20,0),此時OA=20,又由(1)可知當![]() 時,OA=10
時,OA=10![]() ,綜上即可得解.
,綜上即可得解.
(1)過![]() 作直線OE⊥AB于E,則OE=10,設∠EOA=α,則∠EOB=
作直線OE⊥AB于E,則OE=10,設∠EOA=α,則∠EOB=![]() ﹣α,(
﹣α,(![]() ),
),
故AE=10tan![]() ,BE=10tan(
,BE=10tan(![]() ﹣
﹣![]() ),
),
AB=10tan![]() +10tan(
+10tan(![]() ﹣
﹣![]() )=10(
)=10(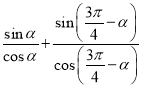 )=
)=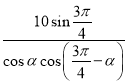 ,
,
又cos![]() =cos
=cos![]() (﹣
(﹣![]() cos
cos![]() +
+![]() sin
sin![]() )=
)=![]()
由![]() ,可得:2
,可得:2![]() ﹣
﹣![]() ,
,
故cos![]() ,當且僅當2
,當且僅當2![]() ﹣
﹣![]() ,即
,即![]() =
=![]() 時取等號,
時取等號,
此時,AB有最小值為20(![]() ),即兩出入口之間距離的最小值為20(
),即兩出入口之間距離的最小值為20(![]() ).
).
(2)由題意可知直線AB是以![]() 為圓心,10為半徑的圓
為圓心,10為半徑的圓![]() 的切線,根據題意,直線AB與圓C要相離,其臨界位置為直線AB與圓C相切,
的切線,根據題意,直線AB與圓C要相離,其臨界位置為直線AB與圓C相切,
設切點為F,此時直線AB為圓![]() 與圓
與圓![]() 的公切線,因為,出入口A在古建筑群和市中心
的公切線,因為,出入口A在古建筑群和市中心![]() 之間,
之間,
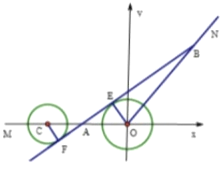
如圖所示,以![]() 為坐標原點,以
為坐標原點,以![]() 所在的直線為
所在的直線為![]() 軸,建立平面直角坐標系
軸,建立平面直角坐標系![]() ,
,
由CF=5,OE=10,因為圓![]() 的方程為x2+y2=100,圓
的方程為x2+y2=100,圓![]() 的方程為(x+30)2+y2=25,
的方程為(x+30)2+y2=25,
設直線AB的方程為y=kx+t(k>0),
則: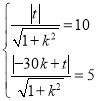 ,所以兩式相除可得:
,所以兩式相除可得:![]() =2,所以t=20k,或t=60k,
=2,所以t=20k,或t=60k,
所以,此時A(﹣20,0)或A(﹣60,0)(舍去),此時OA=20,
又由(1)可知當![]() 時,OA=10
時,OA=10![]() ,綜上,OA
,綜上,OA![]() .
.
即設計出入口A離市中心![]() 的距離在10
的距離在10![]() km到20km之間時,才能使高架道路及其延伸段不經過保護區.
km到20km之間時,才能使高架道路及其延伸段不經過保護區.


 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:
【題目】(本題滿分12分)
今年十一黃金周,記者通過隨機詢問某景區110名游客對景區的服務是否滿意,得到如下的列聯表:
性別與對景區的服務是否滿意 單位:名
男 | 女 | 總計 | |
滿意 | 50 | 30 | 80 |
不滿意 | 10 | 20 | 30 |
總計 | 60 | 50 | 110 |
(1)從這50名女游客中按對景區的服務是否滿意采取分層抽樣,抽取一個容量為5的樣本,問樣本中滿意與不滿意的女游客各有多少名?
(2)從(1)中的5名女游客樣本中隨機選取兩名作深度訪談,求選到滿意與不滿意的女游客各一名的概率;
(3)根據以上列聯表,問有多大把握認為“游客性別與對景區的服務滿意”有關
注:![]()
臨界值表:
P( | 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,圓C經過M(1,3),N(4,2),P(1,﹣7)三點,且直線l:x+ay﹣1=0(a![]() R)是圓C的一條對稱軸,過點A(﹣6,a) 作圓C的一條切線,切點為B,則線段AB的長度為_______.
R)是圓C的一條對稱軸,過點A(﹣6,a) 作圓C的一條切線,切點為B,則線段AB的長度為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過拋物線![]() 的焦點
的焦點![]() 作直線交拋物線于
作直線交拋物線于![]() 兩點,已知點
兩點,已知點![]() ,
,![]() 為坐標原點.若
為坐標原點.若![]() 的最小值為3.
的最小值為3.
(1)求拋物線的方程;
(2)過點![]() 作直線
作直線![]() ,交拋物線于
,交拋物線于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 和點
和點![]() ,直線
,直線![]() ,
,![]() 的斜率乘積為常數
的斜率乘積為常數![]() ,設點
,設點![]() 的軌跡為
的軌跡為![]() ,下列說法正確的是( )
,下列說法正確的是( )
A.存在非零常數![]() ,使
,使![]() 上所有點到兩點
上所有點到兩點![]() ,
,![]() 距離之和為定值
距離之和為定值
B.存在非零常數![]() ,使
,使![]() 上所有點到兩點
上所有點到兩點![]() ,
,![]() 距離之和為定值
距離之和為定值
C.不存在非零常數![]() ,使
,使![]() 上所有點到兩點
上所有點到兩點![]() ,
,![]() 距離之差的絕對值為定值
距離之差的絕對值為定值
D.不存在非零常數![]() ,使
,使![]() 上所有點到兩點
上所有點到兩點![]() ,
,![]() 距離之差的絕對值為定值
距離之差的絕對值為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax+lnx(a∈R),g(x)=x2emx(m∈R,e為自然對數的底數).
(1)討論函數f(x)的單調性及最值;
(2)若a>0,且對x1,x2∈[0,2],f(x1+1)≥g(x2)+a﹣1恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在全國第五個“扶貧日”到來之前,某省開展“精準扶貧,攜手同行”的主題活動,某貧困縣調查基層干部走訪貧困戶數量.甲鎮有基層干部60人,乙鎮有基層干部60人,丙鎮有基層干部80人,每人都走訪了若干貧困戶,按照分層抽樣,從甲、乙、丙三鎮共選20名基層干部,統計他們走訪貧困戶的數量,并將走訪數量分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 5組,繪制成如圖所示的頻率分布直方圖.
5組,繪制成如圖所示的頻率分布直方圖.
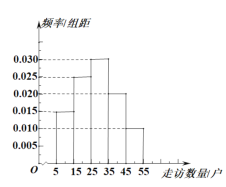
(1)求這20人中有多少人來自丙鎮,并估計甲、乙、丙三鎮的基層干部走訪貧困戶戶數的中位數(精確到整數位);
(2)如果把走訪貧困戶達到或超過35戶視為工作出色,求選出的20名基層干部中工作出色的人數,并從中選2人做交流發言,求這2人中至少有一人走訪的貧困戶在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com