
【題目】已知函數![]() ,函數
,函數![]() .
.
⑴若![]() 的定義域為
的定義域為![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
⑵當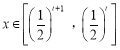 時,求函數
時,求函數![]() 的最小值
的最小值![]() ;
;
⑶是否存在非負實數![]() 、
、![]() ,使得函數
,使得函數![]() 的定義域為
的定義域為![]() ,值域為
,值域為![]() ,若存在,求出
,若存在,求出![]() 、
、![]() 的值;若不存在,則說明理由.
的值;若不存在,則說明理由.
【答案】⑴![]() ;⑵
;⑵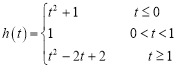 ;⑶存在
;⑶存在![]() 滿足題意.
滿足題意.
【解析】
試題分析:對問題⑴,根據題目條件首先要對實數![]() 的取值進行分類討論,再結合極端不等式恒成立即可求出函數
的取值進行分類討論,再結合極端不等式恒成立即可求出函數![]() 的定義域為
的定義域為![]() 時實數
時實數![]() 的取值范圍;對于問題⑵,根據二次函數的單調性并結合對參數
的取值范圍;對于問題⑵,根據二次函數的單調性并結合對參數![]() 的分類討論,即可求得函數
的分類討論,即可求得函數![]() 的最小值
的最小值![]() ;對問題⑶,根據二次函數的單調性以及函數與方程的思想即可知道存在符合題意的實數
;對問題⑶,根據二次函數的單調性以及函數與方程的思想即可知道存在符合題意的實數![]() 、
、![]() 的值.
的值.
試題解析:⑴![]() 定義域為
定義域為![]() .
.
所以![]() 對一切
對一切![]() 成立. ……………………1分
成立. ……………………1分
當![]() 時,
時,![]() 不可能對一切
不可能對一切![]() 成立. ……………………2分
成立. ……………………2分
所以![]() ,即
,即![]() 解得
解得![]() .
.
綜上![]() . ……………………4分
. ……………………4分
⑵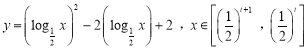 ,
,
令![]() ,
,
所以![]() ……………………5分
……………………5分
當![]() 時,
時,![]() . ……………………6分
. ……………………6分
當![]() 時,
時,![]() . ……………………7分
. ……………………7分
當![]() 時,
時,![]() . ……………………8分
. ……………………8分
所以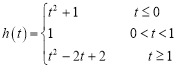 ……………………9分
……………………9分
⑶![]() 在
在![]() 上是增函數,
上是增函數,
若存在非負實數![]() 、
、![]() 滿足題意,則
滿足題意,則![]() ,………………………………10分
,………………………………10分
即![]() 、
、![]() 是方程
是方程![]() 的兩非負實根,且
的兩非負實根,且![]() ,
,
所以![]() .
.
即存在![]() 滿足題意………………………………12分.
滿足題意………………………………12分.


科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() .
.
(1)若方程![]() 有三個解,試求實數
有三個解,試求實數![]() 的取值范圍;
的取值范圍;
(2)是否存在實數![]() ,
,![]() (
(![]() ),使函數
),使函數![]() 的定義域與值域均為
的定義域與值域均為![]() ?若存在,求出所有的區間
?若存在,求出所有的區間![]() ,若不存在,說明理由.
,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的右焦點為
的右焦點為![]() ,離心率
,離心率![]() ,過點
,過點![]() 且垂直于
且垂直于![]() 軸的直線被橢圓
軸的直線被橢圓![]() 截得的弦長為1.
截得的弦長為1.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)記橢圓![]() 的上,下頂點分別為A,B,設過點
的上,下頂點分別為A,B,設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 分別交于點
分別交于點![]() ,求證:直線
,求證:直線![]() 必定過一定點,并求該定點的坐標.
必定過一定點,并求該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面是一段演繹推理:
大前提:如果直線平行于平面,則這條直線平行于平面內的所有直線;
小前提:已知直線b∥平面α,直線a平面α;
結論:所以直線b∥直線a.在這個推理中( )
A. 大前提正確,結論錯誤 B. 大前提錯誤,結論錯誤
C. 大、小前提正確,只有結論錯誤 D. 小前提與結論都是錯誤的
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個地區共有5個鄉鎮,共30萬人,其人口比例為3∶2∶5∶2∶3,從這30萬人中抽取一個300人的樣本,分析某種疾病的發病率.已知這種疾病與不同的地理位置及水土有關,則應采取什么樣的抽樣方法?并寫出具體過程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體![]() 中,棱長
中,棱長![]() ,過點
,過點![]() 的平面
的平面![]() 與正方體的面相交,交線圍成一個正三角形.
與正方體的面相交,交線圍成一個正三角形.

(1)在圖中畫出這個正三角形(不必說明畫法和理由);
(2)平面![]() 將該正方體截成兩個幾何體,求體積較大的幾何體的體積和表面積.
將該正方體截成兩個幾何體,求體積較大的幾何體的體積和表面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列表述正確的是( )
①歸納推理是由部分到整體的推理; ②歸納推理是由一般到一般的推理;
③演繹推理是由一般到特殊的推理; ④類比推理是由特殊到一般的推理;
⑤類比推理是由特殊到特殊的推理.
A. ①②③ B. ②③④ C. ②④⑤ D. ①③⑤
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們把平面幾何里相似的概念推廣到空間:如果兩個幾何體大小不一定相等,但形狀完全相同,就稱它們是相似體,給出下面的幾何體:
①兩個球體;②兩個長方體;③兩個正四面體;④兩個正三棱柱;⑤兩個正四棱錐,則一定是相似體的個數是( )
A. 4 B. 2 C. 3 D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】讀下面的程序:
i=1
S=0
DO
INPUT x
S=S+x
i=i+1
LOOP UNTIL i>10
A=S/10
PRINT A
END
該程序的作用是
A. 計算9個數的和 B. 計算9個數的平均數
C. 計算10個數的和 D. 計算10個數的平均數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com