
【題目】已知![]() 是數列
是數列![]() 的前n項和,
的前n項和,![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)對于正整數![]() ,已知
,已知![]() 成等差數列,求正整數
成等差數列,求正整數![]() 的值;
的值;
(3)設數列![]() 前n項和是
前n項和是![]() ,且滿足:對任意的正整數n,都有等式
,且滿足:對任意的正整數n,都有等式![]() 成立.求滿足等式
成立.求滿足等式![]() 的所有正整數n.
的所有正整數n.
【答案】(1)![]() (2)
(2)![]() (3)1和3.
(3)1和3.
【解析】
試題(1)先根據和項與通項關系得項之間遞推關系,再根據等比數列定義判斷,最后根據等比數列通項公式求結果,(2)根據等差數列化簡得![]() ,再根據正整數限制條件以及指數性質確定不定方程正整數解,(3)先根據定義求數列
,再根據正整數限制條件以及指數性質確定不定方程正整數解,(3)先根據定義求數列![]() 通項公式,再根據等差數列求和公式求
通項公式,再根據等差數列求和公式求![]() ,根據數列相鄰項關系確定
,根據數列相鄰項關系確定![]() 遞減,最后根據單調性求正整數解.
遞減,最后根據單調性求正整數解.
試題解析:(1)由![]()
![]() 得
得![]() ,兩式作差得
,兩式作差得![]() ,即
,即![]()
![]() .
.
![]() ,
,![]() ,所以
,所以![]()
![]() ,
,![]() ,則
,則![]()
![]() ,所以數列
,所以數列![]() 是首項為
是首項為![]() 公比為
公比為![]() 的等比數列,所以
的等比數列,所以![]()
![]() ;
;
(2)由題意![]() ,即
,即![]() ,
,
所以![]() ,其中
,其中![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,所以
,所以![]() ,
,![]() ,
,![]() ;
;
(3)由![]()
![]()
![]() 得,
得,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() ,
,
所以![]()
![]() ,即
,即![]() ,
,
所以![]()
![]() ,
,
又因為![]() ,得
,得![]() ,所以
,所以![]()
![]() ,
,
從而![]()
![]()
![]() ,
,![]() ,
,
當![]() 時
時![]() ;當
;當![]() 時
時![]() ;當
;當![]() 時
時![]() ;
;
下面證明:對任意正整數![]() 都有
都有![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
當![]() 時,
時,![]()
![]() ,即
,即![]() ,
,
所以當![]() 時,
時,![]() 遞減,所以對任意正整數
遞減,所以對任意正整數![]() 都有
都有![]() ;
;
綜上可得,滿足等式![]() 的正整數
的正整數![]() 的值為
的值為![]() 和
和![]() .
.


科目:高中數學 來源: 題型:
【題目】要得到函數![]() 的圖象, 只需將函數
的圖象, 只需將函數![]() 的圖象( )
的圖象( )
A. 所有點的橫坐標伸長到原來的2倍(縱坐標不變), 再將所得的圖像向左平移![]() 個單位.
個單位.
B. 所有點的橫坐標伸長到原來的2倍(縱坐標不變), 再將所得的圖像向左平移![]() 個單位.
個單位.
C. 所有點的橫坐標縮短到原來的![]() 倍(縱坐標不變), 再將所得的圖像向左平移
倍(縱坐標不變), 再將所得的圖像向左平移![]() 個單位.
個單位.
D. 所有點的橫坐標縮短到原來的![]() 倍(縱坐標不變), 再將所得的圖像向左平移
倍(縱坐標不變), 再將所得的圖像向左平移![]() 個單位.
個單位.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電視節目為選拔出現場錄制嘉賓,在眾多候選人中隨機抽取100名選手,按選手身高分組,得到的頻率分布表如圖所示.

(1)請補充頻率分布表中空白位置相應數據,再在答題紙上完成下列頻率分布直方圖;
組號 | 分組 | 頻數 | 頻率 |
第1組 |
| 5 | 0.050 |
第2組 |
| 0.350 | |
第3組 |
| 30 | |
第4組 |
| 20 | 0.200 |
第5組 |
| 10 | 0.100 |
合計 | 100 | 1.00 | |
(2)為選拔出舞臺嘉賓,決定在第3、4、5組中用分層抽樣抽取6人上臺,求第3、4、5組每組各抽取多少人?
(3)求選手的身高平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
如圖,在三棱錐P—ABC中,PC⊥底面ABC,AB⊥BC,D,E分別是AB,PB的中點.

(Ⅰ)求證:DE∥平面PAC.
(Ⅱ)求證:AB⊥PB;
(Ⅲ)若PC=BC,求二面角P—AB—C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)直接寫出![]() 的零點;
的零點;
(2)在坐標系中,畫出![]() 的示意圖(注意要畫在答題紙上)
的示意圖(注意要畫在答題紙上)
(3)根據圖象討論關于![]() 的方程
的方程![]() 的解的個數:
的解的個數:
(4)若方程![]() ,有四個不同的根
,有四個不同的根![]() 、
、![]() 、
、![]() 、
、![]() 直接寫出這四個根的和;
直接寫出這四個根的和;
(5)若函數![]() 在區間
在區間![]() 上既有最大值又有最小值,直接寫出a的取值范圍.
上既有最大值又有最小值,直接寫出a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,
,![]() ,且對所有的實數
,且對所有的實數![]() ,等式
,等式![]() 都成立,其
都成立,其![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() .
.
(1)如果函數![]() ,
,![]() ,求實數
,求實數![]() 的值;
的值;
(2)設函數![]() ,直接寫出滿足
,直接寫出滿足![]() 的兩個函數
的兩個函數![]() ;
;
(3)如果方程![]() 無實數解,求證:方程
無實數解,求證:方程![]() 無實解.
無實解.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區某農產品近幾年的產量統計如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代碼t | 1 | 2 | 3 | 4 | 5 | 6 |
年產量y(萬噸) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根據表中數據,建立![]() 關于的線性回歸方程
關于的線性回歸方程![]() ;
;
(Ⅱ)根據線性回歸方程預測2019年該地區該農產品的年產量.
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: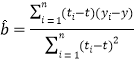 ,
,![]() .(參考數據:
.(參考數據:![]() ,計算結果保留小數點后兩位)
,計算結果保留小數點后兩位)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com