
【題目】已知函數 ![]() .
.
(1)若 ![]() ,討論函數
,討論函數 ![]() 的單調性;
的單調性;
(2)曲線 ![]() 與直線
與直線 ![]() 交于
交于 ![]() ,
, ![]() 兩點,其中
兩點,其中 ![]() ,若直線
,若直線 ![]() 斜率為
斜率為 ![]() ,求證:
,求證: ![]() .
.
【答案】
(1)![]()
, ![]() ,當a≥0時,恒有
,當a≥0時,恒有 ![]() ,
, ![]() 在區間
在區間 ![]() 內是增函數;
內是增函數;
當a<0時,令 ![]() ,即
,即 ![]() ,解得
,解得 ![]() ,令
,令 ![]() 即
即 ![]() ,解得
,解得 ![]() ,綜上,當a≥0時,
,綜上,當a≥0時, ![]() 在區間
在區間 ![]() 內是增函數;
內是增函數;
當a<0時, ![]() 在
在 ![]() 內是增函數,在
內是增函數,在 ![]() 內是減函數.
內是減函數.
(2)
證明: ![]() ,要證明
,要證明 ![]() ,
,
即證 ![]() ,等價于
,等價于 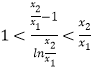 ,令
,令 ![]() (由
(由 ![]() ,知t>1),
,知t>1),
則只需證 ![]() ,由t>1,知
,由t>1,知 ![]() ,故等價于
,故等價于 ![]() (*)
(*)
①令 ![]() ,則
,則 ![]() ,所以
,所以 ![]() 在
在 ![]() 內是增函數,當t>1時,
內是增函數,當t>1時, ![]() ,所以
,所以 ![]() ;
;
②令 ![]() 則
則 ![]() ,所以
,所以 ![]() 在
在 ![]() 內是增函數,當t>1時,
內是增函數,當t>1時, ![]() ,即
,即 ![]() .
.
由①②知(*)成立,所以 ![]() .
.
【解析】本題考查利用導數求函數的單調性、極值、最值,函數與方程、不等式等基礎知識,意在考查綜合分析問題、解決問題的能力和基本運算能力.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:高中數學 來源: 題型:
【題目】已知A={x|x2-ax+a2-19=0},B={ x|x2-5x+6=0},C={x|x2+2x-8=0},且![]()
![]() (A∩B),A∩C=
(A∩B),A∩C=![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點與拋物線
的右焦點與拋物線![]() 的焦點重合,且該橢圓的離心率與雙曲線
的焦點重合,且該橢圓的離心率與雙曲線![]() 的離心率互為倒數.
的離心率互為倒數.
(1)求橢圓的方程;
(2)設直線![]() 與橢圓相交于不同的兩點
與橢圓相交于不同的兩點![]() ,已知點
,已知點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在線段
在線段![]() 的垂直平分線上,且
的垂直平分線上,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]()
(1)設![]() ,
,![]() ,若函數
,若函數![]() 存在零點,求a的取值范圍;
存在零點,求a的取值范圍;
(2)若![]() 是偶函數,求
是偶函數,求![]() 的值;
的值;
(3)在(2)條件下,設![]() ,若函數
,若函數![]() 與
與![]() 的圖象只有一個公共點,求實數b的取值范圍.
的圖象只有一個公共點,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知互不重合的直線![]() ,互不重合的平面
,互不重合的平面![]() ,給出下列四個命題,正確命題的個數是
,給出下列四個命題,正確命題的個數是
①若![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,則
,則![]()
![]()
![]()
②若![]() ,
,![]() ,
,![]() 則
則![]()
③若![]() ,
,![]() ,
,![]() ,則
,則![]()
④若![]()
![]()
![]() ,
,![]()
![]()
![]() ,則
,則![]() //
//![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,D是AC的中點,A1D⊥平面ABC,AB=BC,平面BB1D與棱A1C1交于點E.
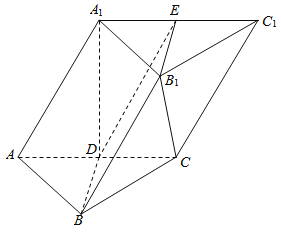
(1)求證:AC⊥A1B;
(2)求證:平面BB1D⊥平面AA1C1C;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c分別為銳角△ABC三個內角A,B,C的對邊,且(a+b)(sinA﹣sinB)=(c﹣b)sinC (Ⅰ)求∠A的大小;
(Ⅱ)若f(x)= ![]() sin
sin ![]() cos
cos ![]() +cos2
+cos2 ![]() ,求f(B)的取值范圍.
,求f(B)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A、B均為銳角,則cosA>sinB是△ABC為鈍角三角形的( )
A.充分不必要條件
B.必要不充分條件
C.充要條件
D.既不充分也不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com