
【題目】若函數(shù)![]() 為常數(shù),
為常數(shù),![]() )的圖象關(guān)于直線
)的圖象關(guān)于直線![]() 對稱,則函數(shù)
對稱,則函數(shù)![]() 的圖象( )
的圖象( )
A. 關(guān)于直線![]() 對稱B. 關(guān)于直線
對稱B. 關(guān)于直線![]() 對稱
對稱
C. 關(guān)于點![]() 對稱D. 關(guān)于點
對稱D. 關(guān)于點![]() 對稱
對稱
【答案】D
【解析】
利用三角函數(shù)的對稱性求得a的值,可得g(x)的解析式,再代入選項,利用正弦函數(shù)的圖象的對稱性,得出結(jié)論.
解:∵函數(shù)f(x)=asinx+cosx(a為常數(shù),x∈R)的圖象關(guān)于直線x=![]() 對稱,
對稱,
∴f(0)=f(![]() ),即
),即![]() ,∴a=
,∴a=![]() ,
,
所以函數(shù)g(x)=sinx+acosx=sinx+![]() cosx=
cosx=![]() sin(x+
sin(x+![]() ),
),
當x=﹣![]() 時,g(x)=-
時,g(x)=-![]() ,不是最值,故g(x)的圖象不關(guān)于直線x=﹣
,不是最值,故g(x)的圖象不關(guān)于直線x=﹣![]() 對稱,故A錯誤,
對稱,故A錯誤,
當x=![]() 時,g(x)=1,不是最值,故g(x)的圖象不關(guān)于直線x=
時,g(x)=1,不是最值,故g(x)的圖象不關(guān)于直線x=![]() 對稱,故B錯誤,
對稱,故B錯誤,
當x=![]() 時,g(x)=
時,g(x)=![]() ≠0,故C錯誤,
≠0,故C錯誤,
當x=![]() 時,g(x)=0,故D正確,
時,g(x)=0,故D正確,
故選:D.


科目:高中數(shù)學 來源: 題型:
【題目】為了解某中學學生對《中華人民共和國交通安全法》的了解情況,調(diào)查部門在該校進行了一次問卷調(diào)查(共12道題),從該校學生中隨機抽取40人,統(tǒng)計了每人答對的題數(shù),將統(tǒng)計結(jié)果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六組,得到如下頻率分布直方圖.
六組,得到如下頻率分布直方圖.
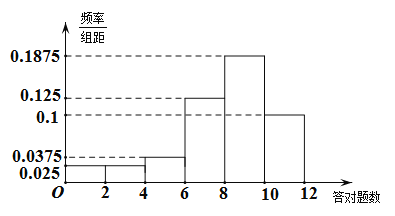
(1)估計這組數(shù)據(jù)的平均數(shù)(同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表);
(2)若從答對題數(shù)在![]() 內(nèi)的學生中隨機抽取2人,求恰有1人答對題數(shù)在
內(nèi)的學生中隨機抽取2人,求恰有1人答對題數(shù)在![]() 內(nèi)的概率.
內(nèi)的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 的內(nèi)角
的內(nèi)角![]() 、
、![]() 、
、![]() 的對邊分別為
的對邊分別為![]() 、
、![]() 、
、![]() ,
,![]() 為
為![]() 內(nèi)一點,若分別滿足下列四個條件:
內(nèi)一點,若分別滿足下列四個條件:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
則點![]() 分別為
分別為![]() 的( )
的( )
A.外心、內(nèi)心、垂心、重心B.內(nèi)心、外心、垂心、重心
C.垂心、內(nèi)心、重心、外心D.內(nèi)心、垂心、外心、重心
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() 過點
過點![]() ,
,![]() 是拋物線
是拋物線![]() 上不同兩點,且
上不同兩點,且![]() (其中
(其中![]() 是坐標原點),直線
是坐標原點),直線![]() 與
與![]() 交于點
交于點![]() ,線段
,線段![]() 的中點為
的中點為![]() .
.
(Ⅰ)求拋物線![]() 的準線方程;
的準線方程;
(Ⅱ)求證:直線![]() 與
與![]() 軸平行.
軸平行.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了了解校園噪音情況,學校環(huán)保協(xié)會對校園噪音值(單位:分貝)進行了![]() 天的監(jiān)測,得到如下統(tǒng)計表:
天的監(jiān)測,得到如下統(tǒng)計表:
噪音值(單位:分貝) |
|
|
|
|
|
|
頻數(shù) |
|
|
|
|
|
|
(1)根據(jù)該統(tǒng)計表,求這![]() 天校園噪音值的樣本平均數(shù)(同一組的數(shù)據(jù)用該組組間的中點值作代表).
天校園噪音值的樣本平均數(shù)(同一組的數(shù)據(jù)用該組組間的中點值作代表).
(2)根據(jù)國家聲環(huán)境質(zhì)量標準:“環(huán)境噪音值超過![]() 分貝,視為重度噪音污染;環(huán)境噪音值不超過
分貝,視為重度噪音污染;環(huán)境噪音值不超過![]() 分貝,視為度噪音污染.”如果把由上述統(tǒng)計表算得的頻率視作概率,回答下列問題:
分貝,視為度噪音污染.”如果把由上述統(tǒng)計表算得的頻率視作概率,回答下列問題:
(i)求周一到周五的五天中恰有兩天校園出現(xiàn)重度噪音污染而其余三天都是輕度噪音污染的概率.
(ii)學校要舉行為期![]() 天的“漢字聽寫大賽”校園選拔賽,把這
天的“漢字聽寫大賽”校園選拔賽,把這![]() 天校園出現(xiàn)的重度噪音污染天數(shù)記為
天校園出現(xiàn)的重度噪音污染天數(shù)記為![]() ,求
,求![]() 的分布列和方差
的分布列和方差![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】給出下列四個說法,其中正確的是( )
A.命題“若![]() ,則
,則![]() ”的否命題是“若
”的否命題是“若![]() ,則
,則![]() ”
”
B.“![]() ”是“雙曲線
”是“雙曲線![]() 的離心率大于
的離心率大于![]() ”的充要條件
”的充要條件
C.命題“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命題“在![]() 中,若
中,若![]() ,則
,則![]() 是銳角三角形”的逆否命題是假命題
是銳角三角形”的逆否命題是假命題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,右焦點為
,右焦點為![]() ,以原點
,以原點![]() 為圓心,橢圓
為圓心,橢圓![]() 的短半軸長為半徑的圓與直線
的短半軸長為半徑的圓與直線![]() 相切.
相切.
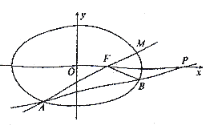
(1)求橢圓![]() 的方程;
的方程;
(2)如圖,過定點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,連接
兩點,連接![]() 并延長交
并延長交![]() 于
于![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com