
【題目】已知曲線![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作直線
作直線![]() 和曲線
和曲線![]() 交于
交于![]() 、
、![]() 兩點(diǎn).
兩點(diǎn).
(1)求曲線![]() 的焦點(diǎn)到它的漸近線之間的距離;
的焦點(diǎn)到它的漸近線之間的距離;
(2)若![]() ,點(diǎn)
,點(diǎn)![]() 在第一象限,
在第一象限,![]() 軸,垂足為
軸,垂足為![]() ,連結(jié)
,連結(jié)![]() ,求直線
,求直線![]() 傾斜角的取值范圍;
傾斜角的取值范圍;
(3)過(guò)點(diǎn)![]() 作另一條直線
作另一條直線![]() ,
,![]() 和曲線
和曲線![]() 交于
交于![]() 、
、![]() 兩點(diǎn),問(wèn)是否存在實(shí)數(shù)
兩點(diǎn),問(wèn)是否存在實(shí)數(shù)![]() ,使得
,使得![]() 和
和![]() 同時(shí)成立?如果存在,求出滿足條件的實(shí)數(shù)
同時(shí)成立?如果存在,求出滿足條件的實(shí)數(shù)![]() 的取值集合,如果不存在,請(qǐng)說(shuō)明理由.
的取值集合,如果不存在,請(qǐng)說(shuō)明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在,實(shí)數(shù)
(3)存在,實(shí)數(shù)![]() 的取值集合為
的取值集合為![]()
【解析】
(1)求出曲線![]() 的焦點(diǎn)和漸近線方程,利用點(diǎn)到直線的距離公式求求解即可;
的焦點(diǎn)和漸近線方程,利用點(diǎn)到直線的距離公式求求解即可;
(2)設(shè)![]() ,
,![]() ,表示出直線
,表示出直線![]() 的斜率,根據(jù)
的斜率,根據(jù)![]() 的范圍,求出其范圍,進(jìn)而得到傾斜角的取值范圍;
的范圍,求出其范圍,進(jìn)而得到傾斜角的取值范圍;
(3)直接求出當(dāng)直線![]() ,直線
,直線![]() 和當(dāng)直線
和當(dāng)直線![]() ,直線
,直線![]() 時(shí),
時(shí),![]() 的值,當(dāng)
的值,當(dāng)![]() 時(shí),與雙曲線聯(lián)立可得
時(shí),與雙曲線聯(lián)立可得![]() ,利用弦長(zhǎng)公式求出
,利用弦長(zhǎng)公式求出![]() 和
和![]() ,利用
,利用![]() 列方程求出
列方程求出![]() 的值,驗(yàn)證判別式成立即可得出結(jié)果.
的值,驗(yàn)證判別式成立即可得出結(jié)果.
(1)曲線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,漸近線方程
,漸近線方程![]() ,
,
由對(duì)稱性,不妨計(jì)算![]() 到直線
到直線![]() 的距離,
的距離,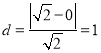 .
.
(2)設(shè)![]() ,
,![]() ,從而
,從而![]()
又因?yàn)辄c(diǎn)![]() 在第一象限,所以
在第一象限,所以![]() ,
,
從而![]() ,
,
所以直線![]() 傾斜角的取值范圍是
傾斜角的取值范圍是![]() ;
;
(3)當(dāng)直線![]() ,直線
,直線![]()
![]() ,
,![]()
當(dāng)直線![]() ,直線
,直線![]() 時(shí),
時(shí),![]()
不妨設(shè)![]() ,與雙曲線聯(lián)立可得
,與雙曲線聯(lián)立可得![]() ,
,
由弦長(zhǎng)公式,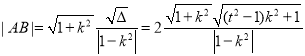
將![]() 替換成
替換成![]() ,可得
,可得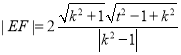
由![]() ,可得
,可得![]() ,
,
解得![]() ,此時(shí)
,此時(shí)![]() 成立.
成立.
因此滿足條件的集合為![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
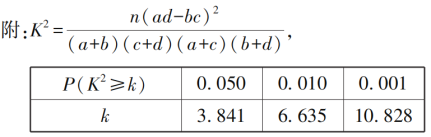
【題目】我們?cè)谇蟾叽畏匠袒虺椒匠痰慕平鈺r(shí)常用二分法求解,在實(shí)際生活中還有三分法.比如借助天平鑒別假幣.有三枚形狀大小完全相同的硬幣,其中有一假幣(質(zhì)量較輕),把兩枚硬幣放在天平的兩端,若天平平衡,則剩余一枚為假幣,若天平不平衡,較輕的一端放的硬幣為假幣.現(xiàn)有 27 枚這樣的硬幣,其中有一枚是假幣(質(zhì)量較輕),如果只有一臺(tái)天平,則一定能找到這枚假幣所需要使用天平的最少次數(shù)為( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為推進(jìn)“千村百鎮(zhèn)計(jì)劃”,![]() 年
年![]() 月某新能源公司開(kāi)展“電動(dòng)莆田 綠色出行”活動(dòng),首批投放
月某新能源公司開(kāi)展“電動(dòng)莆田 綠色出行”活動(dòng),首批投放![]() 臺(tái)
臺(tái)![]() 型新能源車到莆田多個(gè)村鎮(zhèn),供當(dāng)?shù)卮迕衩赓M(fèi)試用三個(gè)月.試用到期后,為了解男女試用者對(duì)
型新能源車到莆田多個(gè)村鎮(zhèn),供當(dāng)?shù)卮迕衩赓M(fèi)試用三個(gè)月.試用到期后,為了解男女試用者對(duì)![]() 型新能源車性能的評(píng)價(jià)情況,該公司要求每位試用者填寫(xiě)一份性能綜合評(píng)分表(滿分為
型新能源車性能的評(píng)價(jià)情況,該公司要求每位試用者填寫(xiě)一份性能綜合評(píng)分表(滿分為![]() 分).最后該公司共收回
分).最后該公司共收回![]() 份評(píng)分表,現(xiàn)從中隨機(jī)抽取
份評(píng)分表,現(xiàn)從中隨機(jī)抽取![]() 份(其中男、女的評(píng)分表各
份(其中男、女的評(píng)分表各![]() 份)作為樣本,經(jīng)統(tǒng)計(jì)得到如下莖葉圖:
份)作為樣本,經(jīng)統(tǒng)計(jì)得到如下莖葉圖:

(1)求![]() 個(gè)樣本數(shù)據(jù)的中位數(shù)
個(gè)樣本數(shù)據(jù)的中位數(shù)![]() ;
;
(2)已知![]() 個(gè)樣本數(shù)據(jù)的平均數(shù)
個(gè)樣本數(shù)據(jù)的平均數(shù)![]() ,記
,記![]() 與
與![]() 的最大值為
的最大值為![]() .該公司規(guī)定樣本中試用者的“認(rèn)定類型”:評(píng)分不小于
.該公司規(guī)定樣本中試用者的“認(rèn)定類型”:評(píng)分不小于![]() 的為“滿意型”,評(píng)分小于
的為“滿意型”,評(píng)分小于![]() 的為“需改進(jìn)型”.
的為“需改進(jìn)型”.
①請(qǐng)根據(jù)![]() 個(gè)樣本數(shù)據(jù),完成下面
個(gè)樣本數(shù)據(jù),完成下面![]() 列聯(lián)表:
列聯(lián)表:
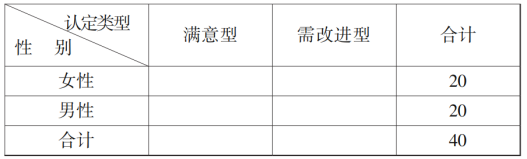
根據(jù)![]() 列聯(lián)表判斷能否有
列聯(lián)表判斷能否有![]() 的把握認(rèn)為“認(rèn)定類型”與性別有關(guān)?
的把握認(rèn)為“認(rèn)定類型”與性別有關(guān)?
②為做好車輛改進(jìn)工作,公司先從樣本“需改進(jìn)型”的試用者按性別用分層抽樣的方法,從中抽取8人進(jìn)行回訪,根據(jù)回訪意見(jiàn)改進(jìn)車輛后,再?gòu)倪@8人中隨機(jī)抽取3人進(jìn)行二次試用,記這3人中男性人數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如題所示:扇形ABC是一塊半徑為2千米,圓心角為60°的風(fēng)景區(qū),P點(diǎn)在弧BC上,現(xiàn)欲在風(fēng)景區(qū)中規(guī)劃三條三條商業(yè)街道PQ、QR、RP,要求街道PQ與AB垂直,街道PR與AC垂直,直線PQ表示第三條街道。
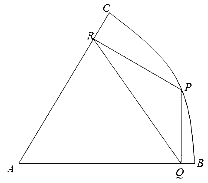
(1)如果P位于弧BC的中點(diǎn),求三條街道的總長(zhǎng)度;
(2)由于環(huán)境的原因,三條街道PQ、PR、QR每年能產(chǎn)生的經(jīng)濟(jì)效益分別為每千米300萬(wàn)元、200萬(wàn)元及400萬(wàn)元,問(wèn):這三條街道每年能產(chǎn)生的經(jīng)濟(jì)總效益最高為多少?(精確到1萬(wàn)元)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)橢圓![]() ,離心率
,離心率![]() ,短軸
,短軸![]() ,拋物線頂點(diǎn)在原點(diǎn),以坐標(biāo)軸為對(duì)稱軸,焦點(diǎn)為
,拋物線頂點(diǎn)在原點(diǎn),以坐標(biāo)軸為對(duì)稱軸,焦點(diǎn)為![]() ,
,
(1)求橢圓和拋物線的方程;
(2)設(shè)坐標(biāo)原點(diǎn)為![]() ,
,![]() 為拋物線上第一象限內(nèi)的點(diǎn),
為拋物線上第一象限內(nèi)的點(diǎn),![]() 為橢圓是一點(diǎn),且有
為橢圓是一點(diǎn),且有![]() ,當(dāng)線段
,當(dāng)線段![]() 的中點(diǎn)在
的中點(diǎn)在![]() 軸上時(shí),求直線
軸上時(shí),求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]()
![]() 的焦點(diǎn)坐標(biāo)分別為
的焦點(diǎn)坐標(biāo)分別為![]() ,
,![]() ,
,![]() 為橢圓
為橢圓![]() 上一點(diǎn),滿足
上一點(diǎn),滿足![]() 且
且![]()
(1) 求橢圓![]() 的標(biāo)準(zhǔn)方程:
的標(biāo)準(zhǔn)方程:
(2) 設(shè)直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() ,若
,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在三棱錐![]() 中,底面是邊長(zhǎng)為
中,底面是邊長(zhǎng)為![]() 的正三角形,點(diǎn)
的正三角形,點(diǎn)![]() 在底面
在底面![]() 上的射影
上的射影![]() 恰是
恰是![]() 的中點(diǎn),側(cè)棱
的中點(diǎn),側(cè)棱![]() 和底面成
和底面成![]() 角.
角.
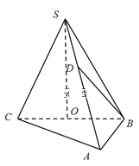
(1)若![]() 為側(cè)棱
為側(cè)棱![]() 上一點(diǎn),當(dāng)
上一點(diǎn),當(dāng)![]() 為何值時(shí),
為何值時(shí),![]() ;
;
(2)求二面角![]() 的余弦值大小.
的余弦值大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義在R上的函數(shù)![]() 滿足
滿足![]() ,且對(duì)任意的
,且對(duì)任意的![]() 都有
都有![]() 其中
其中![]() 為
為![]() 的導(dǎo)數(shù)
的導(dǎo)數(shù)![]() ,則下列一定判斷正確的是( )
,則下列一定判斷正確的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() 底面
底面![]() .
.

(1)當(dāng)![]() 為何值時(shí),
為何值時(shí),![]() 平面
平面![]() ?證明你的結(jié)論;
?證明你的結(jié)論;
(2)若在![]() 邊上至少存在一點(diǎn)
邊上至少存在一點(diǎn)![]() ,使
,使![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com