
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.
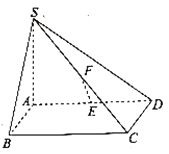
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)證明見解析(2)![]()
【解析】
(1)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,由中位線定理可證,
,由中位線定理可證,![]() ,再由已知條件可得
,再由已知條件可得![]() ,可證四邊形
,可證四邊形![]() 為平行四邊形,即可得證結論;
為平行四邊形,即可得證結論;
(2)![]() 平面
平面![]() ,點
,點![]() 到平面
到平面![]() 的距離相等,轉化為求
的距離相等,轉化為求![]() 到平面
到平面![]() 的距離相等,連接
的距離相等,連接![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,可證
,可證![]() ,結合已知可得
,結合已知可得![]() 平面
平面![]() ,由直線與平面所成角的定義,得
,由直線與平面所成角的定義,得![]() ,根據直角三角形邊角關系及中位線定理,求出
,根據直角三角形邊角關系及中位線定理,求出![]() ,可得
,可得![]() ,由已知條件可得
,由已知條件可得![]() 平面
平面![]() ,進而有
,進而有![]() ,可證
,可證![]() 平面
平面![]() ,
,![]() 為所求距離;或求出三棱錐
為所求距離;或求出三棱錐![]() 的體積和
的體積和![]() 的面積,用等體積法,求點
的面積,用等體積法,求點![]() 到平面
到平面![]() 的距離
的距離
解:(1)證明:如圖,取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,
∴![]() .又∵
.又∵![]() 為
為![]() 中點,底面
中點,底面![]() 是矩形,
是矩形,
∴![]() ,∴
,∴![]() ,
,
∴四邊形![]() 為平行四邊形,∴
為平行四邊形,∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.

(2)方法一:連接![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 與平面
與平面![]() 所成角為
所成角為![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() 為等腰直角三角形,∴
為等腰直角三角形,∴![]() ,
,
∵底面![]() 為矩形,∴
為矩形,∴![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() ,
,![]() ,
,
∴點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.

方法二:連接![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() .
.
在![]() 中,
中,![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() ,在
,在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() 為等腰直角三角形,∴
為等腰直角三角形,∴![]() ,
,
∵底面![]() 為矩形,∴
為矩形,∴![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() .
.
設點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,則
,則
由![]() 得
得![]() .
.
∴![]() ,∴
,∴![]() ,
,
∴點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.



 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,直線l的參數方程為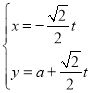 (t為參數,a∈R),以O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρsin2θ=2cosθ
(t為參數,a∈R),以O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρsin2θ=2cosθ
(1)求直線l的普通方程及曲線C的直角坐標方程;
(2)若直線l過點P(1,1)且與曲線C交于AB兩點,求|PA|+|PB|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,兩焦點與短軸的一個端點的連線構成的三角形面積為
,兩焦點與短軸的一個端點的連線構成的三角形面積為![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)設與圓O:![]() 相切的直線l交橢圓C于A,B兩點(O為坐標原點),求△AOB面積的最大值。
相切的直線l交橢圓C于A,B兩點(O為坐標原點),求△AOB面積的最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在棱長為2的正方體![]() 中,點
中,點![]() 是對角線
是對角線![]() 上的點(點
上的點(點![]() 與
與![]() 、
、![]() 不重合),則下列結論正確的個數為( )
不重合),則下列結論正確的個數為( )
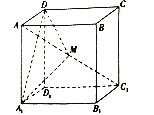
①存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在點![]() ,使得
,使得![]() 平面
平面![]() ;
;
③若![]() 的面積為
的面積為![]() ,則
,則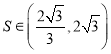 ;
;
④若![]() 、
、![]() 分別是
分別是![]() 在平面
在平面![]() 與平面
與平面![]() 的正投影的面積,則存在點
的正投影的面積,則存在點![]() ,使得
,使得![]() .
.
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知離心率為![]() 的橢圓
的橢圓![]()
![]() 的左頂點為A,且橢圓E經過
的左頂點為A,且橢圓E經過![]() 與坐標軸不垂直的直線l與橢圓E交于C,D兩點,且直線AC和直線AD的斜率之積為
與坐標軸不垂直的直線l與橢圓E交于C,D兩點,且直線AC和直線AD的斜率之積為![]() .
.
(I)求橢圓E的標準方程;
(Ⅱ)求證:直線l過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象在點
的圖象在點![]() 處的切線為
處的切線為![]() ,若函數
,若函數![]() 滿足
滿足![]() (其中
(其中![]() 為函數
為函數![]() 的定義域,當
的定義域,當![]() 時,
時,![]() 恒成立,則稱
恒成立,則稱![]() 為函數
為函數![]() 的“轉折點”,已知函數
的“轉折點”,已知函數![]() 在區間
在區間![]() 上存在一個“轉折點”,則
上存在一個“轉折點”,則![]() 的取值范圍是
的取值范圍是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某餅屋進行為期![]() 天的五周年店慶活動,現策劃兩項有獎促銷活動,活動一:店慶期間每位顧客一次性消費滿
天的五周年店慶活動,現策劃兩項有獎促銷活動,活動一:店慶期間每位顧客一次性消費滿![]() 元,可得
元,可得![]() 元代金券一張;活動二:活動期間每位顧客每天有一次機會獲得一個一元或兩元紅包.根據前一年該店的銷售情況,統計了
元代金券一張;活動二:活動期間每位顧客每天有一次機會獲得一個一元或兩元紅包.根據前一年該店的銷售情況,統計了![]() 位顧客一次性消費的金額數(元),頻數分布表如下圖所示:
位顧客一次性消費的金額數(元),頻數分布表如下圖所示:
一次性消費金額數 |
|
|
|
|
|
人數 |
|
|
|
|
|
以這![]() 位顧客一次消費金額數的頻率分布代替每位顧客一次消費金額數的概率分布.
位顧客一次消費金額數的頻率分布代替每位顧客一次消費金額數的概率分布.
(1)預計該店每天的客流量為![]() 人次,求這次店慶期間,商家每天送出代金券金額數的期望;
人次,求這次店慶期間,商家每天送出代金券金額數的期望;
(2)假設顧客獲得一元或兩元紅包的可能性相等,商家在店慶活動結束后會公布幸運數字,連續![]() 天參加返紅包的顧客,如果紅包金額總數與幸運數字一致,則可再獲得
天參加返紅包的顧客,如果紅包金額總數與幸運數字一致,則可再獲得![]() 元的“店慶幸運紅包”一個.若公布的幸運數字是“
元的“店慶幸運紅包”一個.若公布的幸運數字是“![]() ”,求店慶期間一位連續
”,求店慶期間一位連續![]() 天消費的顧客獲得紅包金額總數的期望.
天消費的顧客獲得紅包金額總數的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】世界軍人運動會,簡稱“軍運會”,是國際軍事體育理事會主辦的全球軍人最高規格的大型綜合性運動會,每四年舉辦一屆,會期7至10天,比賽設27個大項,參賽規模約100多個國家8000余人,規模僅次于奧運會,是和平時期各國軍隊展示實力形象、增進友好交流、擴大國際影響的重要平臺,被譽為“軍人奧運會”.根據各方達成的共識,軍運會于2019年10月18日至27日在武漢舉行,賽期10天,共設置射擊、游泳、田徑、籃球等27個大項、329個小項.其中,空軍五項、軍事五項、海軍五項、定向越野和跳傘5個項目為軍事特色項目,其他項目為奧運項目.現對某國在射擊比賽預賽中的得分數據進行分析,得到如下的頻率分布直方圖:
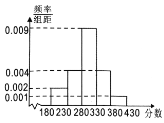
(1)估計某國射擊比賽預賽成績得分的平均值![]() (同一組中的數據用該組區間的中點值代表);
(同一組中的數據用該組區間的中點值代表);
(2)根據大量的射擊成績測試數據,可以認為射擊成績![]() 近似地服從正態分布
近似地服從正態分布![]() ,經計算第(1)問中樣本標準差
,經計算第(1)問中樣本標準差![]() 的近似值為50,用樣本平均數
的近似值為50,用樣本平均數![]() 作為
作為![]() 的近似值,用樣本標準差
的近似值,用樣本標準差![]() 作為
作為![]() 的估計值,求射擊成績得分
的估計值,求射擊成績得分![]() 恰在350到400的概率;[參考數據:若隨機變量
恰在350到400的概率;[參考數據:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則:
,則:![]() ,
,![]() ,
,![]() ;
;
(3)某汽車銷售公司在軍運會期間推廣一款新能源汽車,現面向意向客戶推出“玩游戲,送大獎”,活動,客戶可根據拋擲骰子的結果,操控微型遙控車在方格圖上行進,若遙控車最終停在“勝利大本營”,則可獲得購車優惠券.已知骰子出現任意點數的概率都是![]() ,方格圖上標有第0格,第1格,第2格,……第50格.遙控車開始在第0格,客戶每拋擲一次骰子,遙控車向前移動一次,若拋擲出正面向上的點數是1,2,3,4,5點,遙控車向前移動一格(從
,方格圖上標有第0格,第1格,第2格,……第50格.遙控車開始在第0格,客戶每拋擲一次骰子,遙控車向前移動一次,若拋擲出正面向上的點數是1,2,3,4,5點,遙控車向前移動一格(從![]() 到
到![]() ),若拋擲出正面向上的點數是6點,遙控車向前移動兩格(從
),若拋擲出正面向上的點數是6點,遙控車向前移動兩格(從![]() 到
到![]() ),直到遙控車移動到第49格(勝利大本營)或第50格(失敗大本營)時,游戲結束.設遙控車移動到第
),直到遙控車移動到第49格(勝利大本營)或第50格(失敗大本營)時,游戲結束.設遙控車移動到第![]() 格的概率為
格的概率為![]() ,試證明
,試證明![]() 是等比數列,并求
是等比數列,并求![]() ,以及根據
,以及根據![]() 的值解釋這種游戲方案對意向客戶是否具有吸引力.
的值解釋這種游戲方案對意向客戶是否具有吸引力.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com