
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形,側面
是正方形,側面![]() ⊥底面
⊥底面![]() ,若
,若![]() 分別為
分別為![]() 的中點.
的中點.
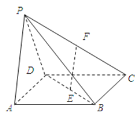
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:平面![]() ⊥平面
⊥平面![]() .
.
【答案】(1)根據題意,證明線面平行,關鍵是先證明線線平行,即![]()
(2)對于面面垂直的證明,一般先證明線面垂直,![]() ,結合面面垂直的判定定理來得到。
,結合面面垂直的判定定理來得到。
【解析】
(Ⅰ)利用線面平行的判定定理,只需證明EF∥PA,即可.
(Ⅱ)先證明線面垂直,CD⊥平面PAD,再證明面面垂直,平面PAD⊥平面PDC即可.
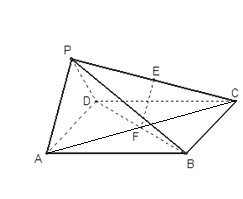
(Ⅰ)證明:連結AC,在正方形ABCD中,F為BD中點,正方形對角線互相平分,
∴F為AC中點,又E是PC中點,在△CPA中,EF∥PA,且PA平面PAD,
EF平面PAD, ∴EF∥平面PAD.
(Ⅱ)∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊥AD,
![]() 平面
平面![]() ∴CD⊥平面PAD,∵CD平面PDC, ∴平面PAD⊥平面PDC
∴CD⊥平面PAD,∵CD平面PDC, ∴平面PAD⊥平面PDC


科目:高中數學 來源: 題型:
【題目】學校舉辦的集體活動中,設計了如下有獎闖關游戲:參賽選手按第一關、第二關、第三關的順序依次闖關,若闖關成功,分別獲得1分、2分、3分的獎勵,游戲還規定,當選手闖過一關后,可以選擇得到相應的分數,結束游戲;也可以選擇繼續闖下一關,若有任何一關沒有闖關成功,則全部分數都歸零,游戲結束。設選手甲第一關、第二關、第三關的概率分別為![]() ,
,![]() ,
,![]() ,選手選擇繼續闖關的概率均為
,選手選擇繼續闖關的概率均為![]() ,且各關之間闖關成功互不影響
,且各關之間闖關成功互不影響
(I)求選手甲第一關闖關成功且所得分數為零的概率
(II)設該學生所得總分數為X,求X的分布列與數學期望
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的右焦點為(
=1(a>b>0)的右焦點為( ![]() ,0),離心率為
,0),離心率為 ![]() .
.
(1)求橢圓C的標準方程;
(2)若動點P(x0 , y0)為橢圓C外一點,且點P到橢圓C的兩條切線相互垂直,求點P的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經過市場調查,某種商品在銷售中有如下關系:第x(1≤x≤30,x∈N+)天的銷售價格(單位:元/件)為f(x)=![]() 第x天的銷售量(單位:件)為g(x)=a-x(a為常數),且在第20天該商品的銷售收入為1 200元(銷售收入=銷售價格×銷售量).
第x天的銷售量(單位:件)為g(x)=a-x(a為常數),且在第20天該商品的銷售收入為1 200元(銷售收入=銷售價格×銷售量).
(1)求a的值,并求第15天該商品的銷售收入;
(2)求在這30天中,該商品日銷售收入y的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2014福建)在下列向量組中,可以把向量 ![]() =(3,2)表示出來的是( )
=(3,2)表示出來的是( )
A.![]() =(0,0),
=(0,0), ![]() =(1,2)
=(1,2)
B.![]() =(﹣1,2),
=(﹣1,2), ![]() =(5,﹣2)
=(5,﹣2)
C.![]() =(3,5),
=(3,5), ![]() =(6,10)
=(6,10)
D.![]() =(2,﹣3),
=(2,﹣3), ![]() =(﹣2,3)
=(﹣2,3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線E: ![]() ﹣
﹣ ![]() =1(a>0,b>0)的兩條漸近線分別為l1:y=2x,l2:y=﹣2x.
=1(a>0,b>0)的兩條漸近線分別為l1:y=2x,l2:y=﹣2x. 
(1)求雙曲線E的離心率;
(2)如圖,O為坐標原點,動直線l分別交直線l1 , l2于A,B兩點(A,B分別在第一、第四象限),且△OAB的面積恒為8,試探究:是否存在總與直線l有且只有一個公共點的雙曲線E?若存在,求出雙曲線E的方程,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程
的極坐標方程![]() ;
;
(Ⅰ)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設![]() 為曲線
為曲線![]() 上的動點,求點
上的動點,求點![]() 到曲線
到曲線![]() 上的距離的最小值的值.
上的距離的最小值的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com