
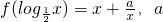 為常數
為常數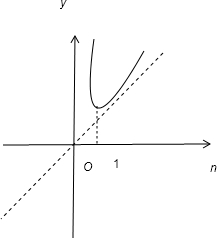 解:(1)∵
解:(1)∵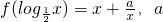 為常數
為常數 則x=
則x=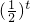
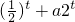 =2-t+a•2t
=2-t+a•2t ,n>0的圖象如圖,
,n>0的圖象如圖, 在(0,1)上單調遞減,在(1,2)單調遞增
在(0,1)上單調遞減,在(1,2)單調遞增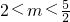 函數有兩個交點
函數有兩個交點 則x=
則x=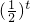 代入可求f(t),以“x“代換“x“可求.
代入可求f(t),以“x“代換“x“可求. ,n>0的圖象,可得方程f(x)=m有兩個實數根x1,x2,其中x1<0,0<x2<1?f(n)=m有兩個實數根n1,n2其中0<n1<1,1<n2<2,結合函數的圖象可得
,n>0的圖象,可得方程f(x)=m有兩個實數根x1,x2,其中x1<0,0<x2<1?f(n)=m有兩個實數根n1,n2其中0<n1<1,1<n2<2,結合函數的圖象可得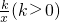 的性質的應用,體現了數形結合思想的應用.
的性質的應用,體現了數形結合思想的應用. 

 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| A、-2 | B、2 | C、4 | D、-4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| A、0 | B、2013 | C、3 | D、-2013 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com