
設函數![]()
![]() .
.
(Ⅰ)試問函數f(x)能否在x= -1時取得極值?說明理由;
(Ⅱ)若a= -1,當x∈[-3,4]時,函數f(x)與g(x)的圖像有兩個公共點,求c的取值范圍.
解:(1) 由題意f′(x)=x2-2ax-a,
假設在x=-1時f(x)取得極值,則有f′(-1)=1+2a-a=0,∴a=-1,………… 4分
而此時,f′(x)=x2+2x+1=(x+1)2≥0,函數f(x)在R上為增函數,無極值.
這與f(x)在x=-1有極值矛盾,所以f(x)在x=-1處無極值.…………………… 6分
(2) 設f(x)=g(x),則有![]() x3-x2-3x-c=0,∴c=
x3-x2-3x-c=0,∴c=![]() x3-x2-3x,
x3-x2-3x,
設F(x)= ![]() x3-x2-3x,G(x)=c,令F′(x)=x2-2x-3=0,解得x1=-1或x=3.
x3-x2-3x,G(x)=c,令F′(x)=x2-2x-3=0,解得x1=-1或x=3.
列表如下:
| x | -3 | (-3,-1) | -1 | (-1,3) | 3 | (3,4) | 4 |
| F′(x) | + | 0 | - | 0 | + | ||
| F(x) | -9 | 增 |
| 減 | -9 | 增 |
|
由此可知:F(x)在(-3,-1)、(3,4)上是增函數,在(-1,3)上是減函數.……………10分
當x=-1時,F(x)取得極大值![]() ;當x=3時,F(x)取得極小值
;當x=3時,F(x)取得極小值
F(-3)=F(3)=-9,而![]() .
.
如果函數f(x)與g(x)的圖像有兩個公共點,則函數F(x)與G(x)有兩個公共點,
所以![]() 或c=-9.………………………………………………15分
或c=-9.………………………………………………15分


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年天津市高考壓軸卷理科數學試卷(解析版) 題型:解答題
設函數 .
.
(1)若 ,試求函數
,試求函數 的單調區間;
的單調區間;
(2)過坐標原點 作曲線
作曲線 的切線,證明:切點的橫坐標為1;
的切線,證明:切點的橫坐標為1;
(3)令 ,若函數
,若函數 在區間(0,1]上是減函數,求
在區間(0,1]上是減函數,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年吉林省高三第六次模擬考試理科數學試卷(解析版) 題型:解答題
已知函數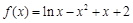 .
.
(Ⅰ)求函數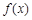 的單調區間;
的單調區間;
(Ⅱ)若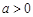 ,求
,求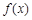 在區間
在區間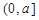 上的最大值;
上的最大值;
(III)設函數
 ,(
,(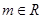 ),試討論函數
),試討論函數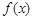 與
與 圖象交點的個數
圖象交點的個數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com