(本小題滿分8分)
某商店經(jīng)營的消費品進價每件14元，月銷售量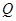
（百件）與銷售價格
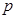（元）的關(guān)系如下圖，每月各種開支2000元.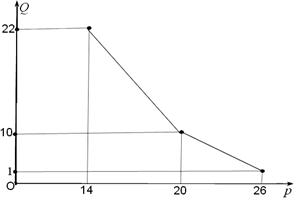
（1）寫出月銷售量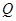（百件）與銷售價格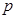（元）的函數(shù)關(guān)系；
（2）寫出月利潤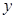
（元）與銷售價格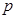（元）的函數(shù)關(guān)系；
（3）當(dāng)商品價格每件為多少元時，月利潤最大？并求出最大值.
（1）
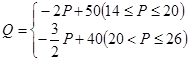（2）
（3）當(dāng)商品價格為19.5元時，利潤最大，為4050元
解析試題分析：（1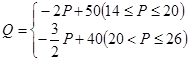） ……………………2分
（2）當(dāng)
時，y=100（P-14）（-2P+50）-2000
即
當(dāng)
時，y="100(p-14)(" 
p+40)-2000
即
…………………4分
所以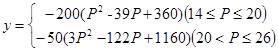
……………5分
（3）當(dāng)商品價格為19.5元時，利潤最大，為4050元………………8分
考點：本題考查了函數(shù)的實際運用
點評：題是由一段一次函數(shù)、一段二次函數(shù)構(gòu)成的分段函數(shù)的最值問題，對于分段函數(shù)的最值，應(yīng)先在各自的定義域上求出各段的最值，然后加以比較，最后確定出最值
閱讀快車系列答案科目：高中數(shù)學(xué) 來源： 題型：解答題
（本題滿分12分）
已知函數(shù)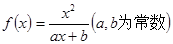
，且方程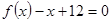
有兩個實根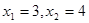
.
（1）求函數(shù)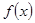
的解析式；
（2）設(shè)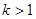
，解關(guān)于
的不等式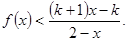
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
已知
是由滿足下述條件的函數(shù)構(gòu)成的集合：對任意
，
① 方程
有實數(shù)根；② 函數(shù)
的導(dǎo)數(shù)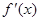
滿足
．
（Ⅰ）判斷函數(shù)
是否是集合中的元素，并說明理由；
（Ⅱ）集合中的元素具有下面的性質(zhì)：若的定義域為
，則對于任意
，都存在
，使得等式
成立．試用這一性質(zhì)證明：方程有且只有一個實數(shù)根；
（Ⅲ）對任意，且
，求證：對于定義域中任意的
，
，
，當(dāng)
，且
時，
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
已知函數(shù)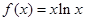
，
．
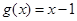（Ⅰ）求函數(shù)
的單調(diào)區(qū)間；
（Ⅱ）若對任意正實數(shù)x，不等式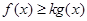
恒成立，求實數(shù)k的值；
（Ⅲ）求證：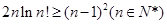
．（其中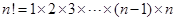
）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
（本小題滿分14分）
設(shè)函數(shù)
（
為實常數(shù)）為奇函數(shù)，函數(shù)
．
（Ⅰ）求的值；
（Ⅱ）求
在
上的最大值；
（Ⅲ）當(dāng)
時，
對所有的
及
恒成立，求實數(shù)
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
(12分)我們把同時滿足下列兩個性質(zhì)的函數(shù)稱為“和諧函數(shù)” :
①函數(shù)在整個定義域上是單調(diào)增函數(shù)或單調(diào)減函數(shù);
②在函數(shù)的定義域內(nèi)存在區(qū)間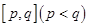
,使得函數(shù)在區(qū)間
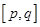上的值域為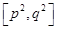
.
⑴已知冪函數(shù)
的圖像經(jīng)過點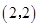
,判斷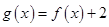
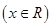是否是和諧函數(shù)?
⑵判斷函數(shù)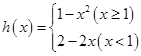
是否是和諧函數(shù)?
⑶若函數(shù)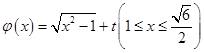
是和諧函數(shù),求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
設(shè)函數(shù)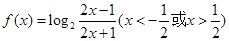
.
(1)證明: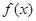
是奇函數(shù);
(2)求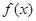的單調(diào)區(qū)間;
(3)寫出函數(shù)
圖象的一個對稱中心.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的極值；
時，
，且
，求證：