
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,圓
,圓![]() :
:![]() 過橢圓
過橢圓![]() 的三個頂點,過點
的三個頂點,過點![]() 的直線
的直線![]() (斜率存在且不為0)與橢圓
(斜率存在且不為0)與橢圓![]() 交于
交于![]() 兩點.
兩點.
(1)求橢圓![]() 的標準方程.
的標準方程.
(2)證明:在![]() 軸上存在定點
軸上存在定點![]() ,使得
,使得![]() 為定值,并求出定點
為定值,并求出定點![]() 的坐標.
的坐標.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】給出下列五個命題:
①直線![]() 平行于平面
平行于平面![]() 內的一條直線,則
內的一條直線,則![]() ;
;
②若![]() 是銳角三角形,則
是銳角三角形,則![]() ;
;
③已知![]() 是等差數列
是等差數列![]() 的前
的前![]() 項和,若
項和,若![]() ,則
,則![]() ;
;
④當![]() 時,不等式
時,不等式![]() 恒成立,則實數
恒成立,則實數![]() 的取值范圍為
的取值范圍為![]() .
.
其中正確命題的序號為___________.
查看答案和解析>>
科目:高中數學 來源: 題型:
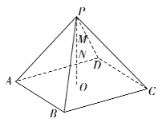
【題目】如圖,在四棱錐![]() 中,頂點P在底面的投影
中,頂點P在底面的投影![]() 恰為正方形ABCD的中心且
恰為正方形ABCD的中心且![]() ,設點M,N分別為線段PD,PO上的動點,已知當
,設點M,N分別為線段PD,PO上的動點,已知當![]() 取得最小值時,動點M恰為PD的中點,則該四棱錐的外接球的表面積為____________.
取得最小值時,動點M恰為PD的中點,則該四棱錐的外接球的表面積為____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,直線
,直線![]() 與橢圓C交于A,B兩點,且
與橢圓C交于A,B兩點,且![]() .
.
(1)求橢圓C的方程.
(2)不經過點![]() 的直線
的直線![]() 被圓
被圓![]() 截得的弦長與橢圓C的長軸長相等,且直線
截得的弦長與橢圓C的長軸長相等,且直線![]() 與橢圓C交于D,E兩點,試判斷
與橢圓C交于D,E兩點,試判斷![]() 的周長是否為定值?若是,求出定值;若不是,請說明理由.
的周長是否為定值?若是,求出定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年“非洲豬瘟”過后,全國生豬價格逐步上漲,某大型養豬企業,欲將達到養殖周期的生豬全部出售,根據去年的銷售記錄,得到銷售生豬的重量的頻率分布直方圖(如圖所示).

(1)根據去年生豬重量的頻率分布直方圖,估計今年生豬出欄(達到養殖周期)時,生豬重量達不到270斤的概率(以頻率代替概率);
(2)若假設該企業今年達到養殖周期的生豬出欄量為5000頭,生豬市場價格是30元/斤,試估計該企業本養殖周期的銷售收入是多少萬元;
(3)若從本養殖周期的生豬中,任意選兩頭生豬,其重量達到270斤及以上的生豬數為隨機變量![]() ,試求隨機變量
,試求隨機變量![]() 的分布列及方差.
的分布列及方差.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com