
【題目】選修4-5:不等式選講
已知函數![]() .
.
(1)解不等式![]() ;
;
(2)若關于![]() 的方程
的方程![]() 的解集為空集,求實數
的解集為空集,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() (2)
(2)![]()
【解析】試題分析:(1)根據絕對值定義將不等式化為三個不等式組,分別求解,最后求并集(2)先根據絕對值定義將函數化為分段函數,求對應函數值域,即得f(x)﹣4的取值范圍,根據倒數性質可得![]() 取值范圍,最后根據方程解集為空集,確定實數
取值范圍,最后根據方程解集為空集,確定實數![]() 的取值范圍
的取值范圍
試題解析:解:(1)解不等式|x﹣2|+|2x+1|>5,
x≥2時,x﹣2+2x+1>5,解得:x>2;
﹣![]() <x<2時,2﹣x+2x+1>5,無解,
<x<2時,2﹣x+2x+1>5,無解,
x≤﹣![]() 時,2﹣x﹣2x﹣1>5,解得:x<﹣
時,2﹣x﹣2x﹣1>5,解得:x<﹣![]() ,
,
故不等式的解集是(﹣∞,﹣![]() )∪(2,+∞);
)∪(2,+∞);
(2)f(x)=|x﹣2|+|2x+1|=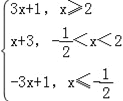 ,
,
故f(x)的最小值是![]() ,所以函數f(x)的值域為[
,所以函數f(x)的值域為[![]() ,+∞),
,+∞),
從而f(x)﹣4的取值范圍是[﹣![]() ,+∞),
,+∞),
進而![]() 的取值范圍是(﹣∞,﹣
的取值范圍是(﹣∞,﹣![]() ]∪(0,+∞).
]∪(0,+∞).
根據已知關于x的方程![]() =a的解集為空集,所以實數a的取值范圍是(﹣
=a的解集為空集,所以實數a的取值范圍是(﹣![]() ,0].
,0].


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,圓![]() 的圓心坐標為
的圓心坐標為![]() ,半徑為2.以極點為原點,極軸為
,半徑為2.以極點為原點,極軸為![]() 的正半軸,取相同的長度單位建立平面直角坐標系,直線
的正半軸,取相同的長度單位建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為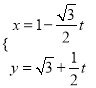 (
(![]() 為參數).
為參數).
(1)求圓![]() 的極坐標方程;
的極坐標方程;
(2)設![]() 與圓
與圓![]() 的交點為
的交點為![]() ,
, ![]() 與
與![]() 軸的交點為
軸的交點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
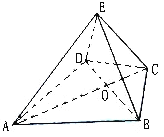
【題目】如圖,在四棱錐![]() 中,
中, ![]() 是正三角形,
是正三角形, ![]() 是等腰三角形,
是等腰三角形, ![]() ,
, ![]() .
.
(1)求證: ![]() ;
;
(2)若![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,直線
,直線![]() 與平面
與平面![]() 所成的角為45°,求二面角
所成的角為45°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
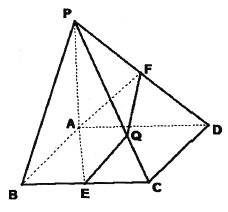
【題目】如圖,在底面是菱形的四棱錐![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,點
,點![]() 分別為
分別為![]() 的中點,設直線
的中點,設直線![]() 與平面
與平面![]() 交于點
交于點![]() .
.
(1)已知平面![]() 平面
平面![]() ,求證:
,求證: ![]() .
.
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的左、右焦點分別為
)的左、右焦點分別為![]() 、
、![]() ,設點
,設點![]() ,在
,在![]() 中,
中, ![]() ,周長為
,周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設不經過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點,若直線
兩點,若直線![]() 與
與![]() 的斜率之和為
的斜率之和為![]() ,求證:直線
,求證:直線![]() 過定點,并求出該定點的坐標;
過定點,并求出該定點的坐標;
(3)記第(2)問所求的定點為![]() ,點
,點![]() 為橢圓
為橢圓![]() 上的一個動點,試根據
上的一個動點,試根據![]() 面積
面積![]() 的不同取值范圍,討論
的不同取值范圍,討論![]() 存在的個數,并說明理由.
存在的個數,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班為了活躍元旦晚會氣氛,主持人請12位同學做一個游戲,第一輪游戲中,主持人將標有數字1到12的十二張相同的卡片放入一個不透明的盒子中,每人依次從中取出一張卡片,取到標有數字7到12的卡片的同學留下,其余的淘汰;第二輪將標有數字1到6的六張相同的卡片放入一個不透明的盒子中,每人依次從中取出一張卡片,取到標有數字4到6的卡片的同學留下,其余的淘汰;第三輪將標有數字1,2,3的三張相同的卡片放入一個不透明的盒子中,每人依次從中取出一張卡片,取到標有數字2,3的卡片的同學留下,其余的淘汰;第四輪用同樣的辦法淘汰一位同學,最后留下的這位同學獲得一個獎品.已知同學甲參加了該游戲.
(1)求甲獲得獎品的概率;
(2)設![]() 為甲參加游戲的輪數,求
為甲參加游戲的輪數,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com