
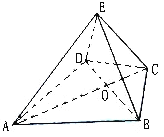
【題目】如圖,在四棱錐![]() 中,
中, ![]() 是正三角形,
是正三角形, ![]() 是等腰三角形,
是等腰三角形, ![]() ,
, ![]() .
.
(1)求證: ![]() ;
;
(2)若![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,直線
,直線![]() 與平面
與平面![]() 所成的角為45°,求二面角
所成的角為45°,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)取BD中點O,連結CO,EO,推導出CO⊥BD,EO⊥BD,由此能證明BE=DE.
(2)以O為原點,OA為x軸,OB為y軸,OE為z軸,建立空間直角坐標系,利用向量法能求出二面角B﹣AE﹣D的余弦值.
試題解析:
證明:(1)取BD中點O,連結CO,EO,
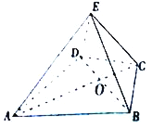
∵△BCD是等腰三角形,∠BCD=120°,∴CB=CD,∴CO⊥BD,
又∵EC⊥BD,EC∩CO=C,∴BD⊥平面EOC,∴EO⊥BD,
在△BDE中,∵O為BD的中點,∴BE=DE.
(2)∵平面EBD⊥平面ABCD,平面EBD∩平面ABCD=BD,
EO⊥BD,∴EO⊥平面ABCD,
又∵CO⊥BD,AO⊥BD,
∴A,O,C三點共線,AC⊥BD,
以O為原點,OA為x軸,OB為y軸,OE為z軸,建立空間直角坐標系,
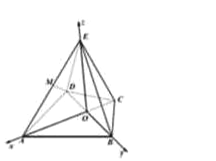
在正△ABD中,AB=2![]() ,∴AO=3,BO=DO=
,∴AO=3,BO=DO=![]() ,
,
∵直線AE與平面ABD所成角為45°,∴EO=AO=3,
A(3,0,0),B(0,![]() ,0),D(0,﹣
,0),D(0,﹣![]() ,0),E(0,0,3),
,0),E(0,0,3),
![]() =(﹣3,
=(﹣3,![]() ,0),
,0),![]() =(﹣3,﹣
=(﹣3,﹣![]() ,0),
,0),![]() =(﹣3,0,3),
=(﹣3,0,3),
設平面ABE的法向量![]() =(a,b,c),
=(a,b,c),
則![]() ,取a=1,得
,取a=1,得![]() =(1,
=(1,![]() ,1),
,1),
設平面ADE的法向量![]() =(x,y,z),
=(x,y,z),
則![]() ,取x=1,得
,取x=1,得![]() =(1,﹣
=(1,﹣![]() ,1),
,1),
設二面角B﹣AE﹣D為θ,
則cosθ=![]() =
=![]() =
=![]() .
.
∴二面角B﹣AE﹣D的余弦值為![]() .
.


科目:高中數學 來源: 題型:
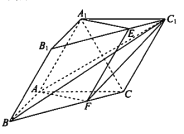
【題目】如圖,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() .過
.過![]() 的平面交
的平面交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .
.
(l)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求證: ![]() ;
;
(Ⅲ)記四棱錐![]() 的體積為
的體積為![]() ,三棱柱
,三棱柱![]() 的體積為
的體積為![]() .若
.若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(1)若曲線![]() 在
在![]() 軸上的截距為
軸上的截距為![]() ,且在點
,且在點![]() 處的切線垂直于直線
處的切線垂直于直線![]() ,求實數
,求實數![]() 的值;
的值;
(2)記![]() 的導函數為
的導函數為![]() ,
, ![]() 在區間
在區間![]() 上的最小值為
上的最小值為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形, ![]() , 平面
, 平面![]() 底面
底面![]() ,且
,且![]() 是邊長為
是邊長為![]() 的等邊三角形,
的等邊三角形, ![]() ,
, ![]() 是
是![]() 中點.
中點.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)證明: ![]() , 且
, 且![]() 與
與![]() 的面積相等.
的面積相等.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機抽取100名學生,測得他們的身高(單位: ![]() ),按照區間
),按照區間![]() ,
,
![]() 分組,得到樣本身高的頻率分布直方圖(如圖).
分組,得到樣本身高的頻率分布直方圖(如圖).

(1)求頻率分布直方圖中![]() 的值及身高在
的值及身高在![]() 以上的學生人數;
以上的學生人數;
(2)將身高在![]() 區間內的學生依次記為
區間內的學生依次記為![]() 三個組,用分層抽樣的方法從這三個組中抽取6人,求從這三個組分別抽取的學生人數;
三個組,用分層抽樣的方法從這三個組中抽取6人,求從這三個組分別抽取的學生人數;
(3)在(2)的條件下,要從6名學生中抽取2人.用列舉法計算![]() 組中至少有1人被抽中的概率.
組中至少有1人被抽中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,
, ![]() ,
, ![]() ,
, ![]() 滿足
滿足![]() ,且當
,且當![]() 時,
時, ![]() ,令
,令![]() .
.
(Ⅰ)寫出![]() 的所有可能的值.
的所有可能的值.
(Ⅱ)求![]() 的最大值.
的最大值.
(Ⅲ)是否存在數列![]() ,使得
,使得![]() ?若存在,求出數列
?若存在,求出數列![]() ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班為了活躍元旦晚會氣氛,主持人請12位同學做一個游戲,第一輪游戲中,主持人將標有數字1到12的十二張相同的卡片放入一個不透明的盒子中,每人依次從中取出一張卡片,取到標有數字7到12的卡片的同學留下,其余的淘汰;第二輪將標有數字1到6的六張相同的卡片放入一個不透明的盒子中,每人依次從中取出一張卡片,取到標有數字4到6的卡片的同學留下,其余的淘汰;第三輪將標有數字1,2,3的三張相同的卡片放入一個不透明的盒子中,每人依次從中取出一張卡片,取到標有數字2,3的卡片的同學留下,其余的淘汰;第四輪用同樣的辦法淘汰一位同學,最后留下的這位同學獲得一個獎品.已知同學甲參加了該游戲.
(1)求甲獲得獎品的概率;
(2)設![]() 為甲參加游戲的輪數,求
為甲參加游戲的輪數,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com