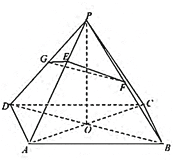
【題目】如圖，在四棱錐
中，
是正三角形，四邊形
是正方形.
（Ⅰ）求證：
；
（Ⅱ）若
，求直線
與平面
所成角的正弦值.
【答案】（I）見解析（II）
【解析】
（Ⅰ）取
的中點(diǎn)
及
的中點(diǎn)
，連結(jié)
，
，
．要證
，即證
；
（Ⅱ）過B作
平面
，垂足為
，連接
，
，
為直線
與平面所成角.
（I）取的中點(diǎn)及的中點(diǎn)，連結(jié)，，．
由△
是正三角形，四邊形
是正方形得
，
，
又
平面
，
，
所以
平面．
因?yàn)?/span>
，所以
平面，
又
平面，所以，
又的中點(diǎn)是，所以．
（II）過B作平面，垂足為，連接，，
為直線與平面所成角，
．
過作
于
，
由平面及
平面，得
，
又，
平面，
，
所以
平面．
由，
平面，
平面，得
平面．
于是點(diǎn)
到平面的距離等于點(diǎn)到平面的距離等于
設(shè)
，則
，
，
計(jì)算得
，
，
在等腰三角形中可算得
，
所以直線與平面所成角的正弦值等于
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】網(wǎng)絡(luò)游戲要實(shí)現(xiàn)可持續(xù)發(fā)展，必須要發(fā)展綠色網(wǎng)游.為此，國家文化部將從內(nèi)容上對網(wǎng)游作出強(qiáng)制規(guī)定，國家信息產(chǎn)業(yè)部還將從技術(shù)上加強(qiáng)對網(wǎng)游的強(qiáng)制限制，開發(fā)限制網(wǎng)癮的疲勞系統(tǒng)，現(xiàn)已開發(fā)的“游戲防沉迷系統(tǒng)”規(guī)則如下：
①
小時(shí)以內(nèi)（含小時(shí)）為健康時(shí)間，玩家在這段時(shí)間內(nèi)獲得的累積經(jīng)驗(yàn)值
（單位：
）與游戲時(shí)間
（小時(shí)）滿足關(guān)系式：
（
為常數(shù)）；
②小時(shí)到
小時(shí)（含小時(shí)）為疲勞時(shí)間，玩家在這段時(shí)間內(nèi)獲得的經(jīng)驗(yàn)值為
（即累積經(jīng)驗(yàn)值不變）；
③超過小時(shí)為不健康時(shí)間，累積經(jīng)驗(yàn)值開始損失，損失的經(jīng)驗(yàn)值與不健康時(shí)間成正比例關(guān)系，比例系數(shù)為
.
（1）當(dāng)
時(shí)，寫出累積經(jīng)驗(yàn)值與游戲時(shí)間的函數(shù)關(guān)系式
，并求出游戲
小時(shí)的累積經(jīng)驗(yàn)值；
（2）定義“玩家愉悅指數(shù)”為累積經(jīng)驗(yàn)值與游戲時(shí)間的比值，記作
；若
，開發(fā)部門希望在健康時(shí)間內(nèi)，這款游戲的“玩家愉悅指數(shù)”不低于
，求實(shí)數(shù)的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知f（x）＝ax+ka﹣x（a＞0且a≠1）是R上的奇函數(shù)，且f（1）
．
（1）求f（x）的解析式；
（2）若關(guān)于x的方程f（
1）+f（1﹣3mx﹣2）＝0在區(qū)間[0，1]內(nèi)只有一個(gè)解，求m取值集合；
（3）是否存在正整數(shù)n，使不得式f（2x）≥（n﹣1）f（x）對一切x∈[﹣1，1]均成立？若存在，求出所有n的值若不存在，說明理由
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知拋物線
的焦點(diǎn)為
，準(zhǔn)線為
，在拋物線
上任取一點(diǎn)
，過做的垂線，垂足為
.
（1）若
，求
的值；
（2）除外，
的平分線與拋物線是否有其他的公共點(diǎn)，并說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
（1）討論函數(shù)
的單調(diào)性；
（2）若函數(shù)
在區(qū)間
上存在兩個(gè)不同零點(diǎn)，求實(shí)數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】四棱錐
中，底面
是邊長為2的菱形，
.
,且
平面，
，點(diǎn)
分別是線段
上的中點(diǎn)，
在
上.且
.
（Ⅰ）求證：
平面
；
（Ⅱ）求直線
與平面的成角的正弦值；
（Ⅲ）請畫出平面與四棱錐的表面的交線，并寫出作圖的步驟.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)
．
（I）若
，求函數(shù)
的單調(diào)區(qū)間．
（II）若函數(shù)
在區(qū)間
上是減函數(shù)，求實(shí)數(shù)
的取值范圍．
（III）過坐標(biāo)原點(diǎn)
作曲線
的切線，求切線的橫坐標(biāo)．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的左右焦點(diǎn)分別為
，若橢圓上一點(diǎn)
滿足
，過點(diǎn)
的直線
與橢圓
交于兩點(diǎn)
.
（1）求橢圓的方程；
（2）過點(diǎn)
作
軸的垂線，交橢圓于
，求證：存在實(shí)數(shù)
，使得
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com
