
【題目】某創業者計劃在某旅游景區附近租賃一套農房發展成特色“農家樂”,為了確定未來發展方向此創業者對該景區附近五家“農家樂”跟蹤調查了100天,這五家“農家樂的收費標準互不相同得到的統計數據如下表,x為收費標準(單位:元/日),t為入住天數(單位:天),以頻率作為各自的“入住率”,收費標準x與“入住率”y的散點圖如圖
x | 100 | 150 | 200 | 300 | 450 |
t | 90 | 65 | 45 | 30 | 20 |
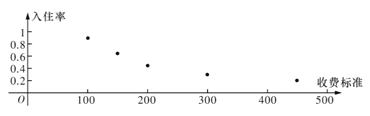
(1)若從以上五家“農家樂”中隨機抽取兩家深人調查,記![]() 為“入住率超過0.6的農家樂的個數,求
為“入住率超過0.6的農家樂的個數,求![]() 的概率分布列
的概率分布列
(2)z=lnx,由散點圖判斷![]() 與
與![]() 哪個更合適于此模型(給出判斷即可不必說明理由)?并根據你的判斷結果求回歸方程(a,
哪個更合適于此模型(給出判斷即可不必說明理由)?并根據你的判斷結果求回歸方程(a,![]() 的結果精確到0.1)
的結果精確到0.1)
(3)根據第(2)問所求的回歸方程,試估計收費標準為多少時,100天銷售額L最大?(100天銷售額L=100×入住率×收費標準x)
參考數據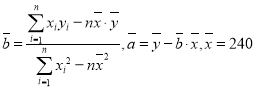 ,
,![]() ,
,![]()
![]()
 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若不等式![]() 的解集為
的解集為![]() ,求不等式
,求不等式![]() 的解集;
的解集;
(2)![]() 時,
時,
①當![]() 時,若不等式
時,若不等式![]() 在
在![]() 有解,求
有解,求![]() 的取值范圍;
的取值范圍;
②當![]() 時,設
時,設![]() ,若存在
,若存在![]() ,
,![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]()
![]() 的一個焦點為
的一個焦點為![]() ,且橢圓
,且橢圓![]() 過點
過點![]() ,
,![]() 為坐標原點,
為坐標原點,
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)是否存在圓心在原點的圓,使得該圓的任意一條切線與橢圓![]() 恒有兩個交點
恒有兩個交點![]() 、
、![]() ,且
,且![]() ?若存在,寫出該圓的方程,并求
?若存在,寫出該圓的方程,并求![]() 的最大值,若不存在說明理由.
的最大值,若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國有十二生肖,又叫十二屬相,每一個人的出生年份對應了十二種動物(鼠、牛、虎、兔、龍、蛇、馬、羊、猴、雞、狗、豬)的一種,現有十二生肖的吉物各一個,甲、乙、丙三位同學依次選一個作為禮物,甲同學喜歡牛和馬,乙同學喜歡牛、兔、狗和羊,丙同學哪個吉祥物都喜歡,如果讓三位同學選取的禮物都滿意,那么不同的選法有( )
A. 50種B. 60種C. 70種D. 90種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知學校高三年級有學生1000名,經調查研究,其中750名同學經常參加體育鍛煉(稱為A類同學),另外250名同學不經常參加體育鍛煉(稱為B類同學). 現用分層抽樣方法(按A類、B類分兩層)從該年級學生中共抽查100名同學,測得這100名同學的身高(單位:![]() )頻率分布直方圖如圖:
)頻率分布直方圖如圖:
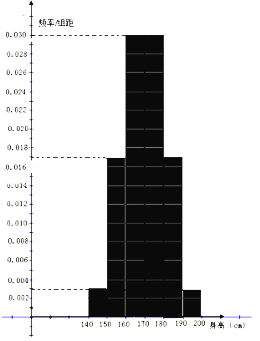
(Ⅰ)以同一組數據常用該組區間的中點值(例如區間![]() 的中點值為165)作為代表,計算這100名學生身高數據的平均值;
的中點值為165)作為代表,計算這100名學生身高數據的平均值;
(Ⅱ)如果以身高不低于![]() 作為達標的標準,對抽取的100名學生,得到以下列聯表:
作為達標的標準,對抽取的100名學生,得到以下列聯表:
身高達標 | 身高不達標 | 總計 | |
積極參加體育鍛煉 | 40 | ||
不積極參加體育鍛煉 | 15 | ||
總計 | 100 |
完成上表,并判斷是否有![]() 的把握認為體育鍛煉與身高達標有關系(
的把握認為體育鍛煉與身高達標有關系(![]() 值精確到0.01)?
值精確到0.01)?
參考公式: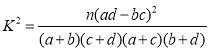
參考數據:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 對定義域中任意x均滿足
對定義域中任意x均滿足![]() ,則稱函數
,則稱函數![]() 的圖象關于點
的圖象關于點![]() 對稱.
對稱.
(1)已知函數![]() 的圖象關于點
的圖象關于點![]() 對稱,求實數m的值;
對稱,求實數m的值;
(2)已知函數![]() 在
在![]() 上的圖象關于點
上的圖象關于點![]() 對稱,且當
對稱,且當![]() 時,
時,![]() ,求函數
,求函數![]() 在
在![]() 上的解析式;
上的解析式;
(3)在(1)(2)的條件下,當![]() 時,若對任意實數
時,若對任意實數![]() ,恒有
,恒有![]() 成立,求實數a的取值范圍.
成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com