【題目】已知
是函數
的零點，
.
（1）求實數
的值；
（2）若不等式
在
上恒成立，求實數
的取值范圍；
（3）若方程
有三個不同的實數解，求實數的取值范圍.
名題金卷系列答案科目：高中數學 來源： 題型：
【題目】交強險是車主必須為機動車購買的險種，若普通6座以下私家車投保交強險第一年的費用（基準保費）統一為
元，在下一年續保時，實行的是費率浮動機制，保費與上一年度車輛發生道路交通事故的情況相聯系，發生交通事故的次數越多，費率也就越高，具體浮動情況如下表：
交強險浮動因素和浮動費率比率表 | ||
浮動因素 | 浮動比率 | |
| 上一個年度未發生有責任道路交通事故 | 下浮10% |
| 上兩個年度未發生責任道路交通事故 | 下浮20% |
| 上三個及以上年度未發生有責任道路交通事故 | 下浮30% |
| 上一個年度發生一次有責任不涉及死亡的道路交通事故 | 0% |
| 上一個年度發生兩次及兩次以上有責任道路交通事故 | 上浮10% |
| 上一個年度發生有責任道路交通死亡事故 | 上浮30% |
某機購為了研究某一品牌普通6座以下私家車的投保情況，隨機抽取了60輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況，統計得到了下面的表格：
類型 |
|
|
|
|
|
|
數量 | 10 | 5 | 5 | 20 | 15 | 5 |
（1）求一輛普通6座以下私家車在第四年續保時保費高于基本保費的頻率；
（2）某二手車銷售商專門銷售這一品牌的二手車，且將下一年的交強險保費高于基本保費的車輛記為事故車，假設購進一輛事故車虧損5000元，一輛非事用戶車盈利10000元，且各種投保類型車的頻率與上述機構調查的頻率一致，完成下列問題：
①若該銷售商店內有六輛（車齡已滿三年）該品牌二手車，某顧客欲在店內隨機挑選兩輛車，求這兩輛車恰好有一輛為事故車的概率；
②若該銷售商一次購進120輛（車齡已滿三年）該品牌二手車，求一輛車盈利的平均值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】小明和爸爸媽媽、爺爺奶奶一同參加《中國詩詞大會》的現場錄制，5人坐成一排.若小 明的父母至少有一人與小明相鄰，則不同的坐法總數為________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的兩個焦點分別為
和
，過點
的直線與橢圓相交與
兩點，且
.
（1）求橢圓的離心率；
（2）求直線
的斜率；
（3）設點
與點
關于坐標原點對稱，直線
上有一點
在
的外接圓上，且
，求橢圓方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
的圖象過點
．
（1）求
的值并求函數
的值域；
（2）若關于
的方程
在
有實根，求實數
的取值范圍；
（3）若函數
，則是否存在實數
，對任意
，存在
使
成立？若存在，求出的取值范圍；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近年來，隨著汽車消費水平的提高，二手車流通行業得到迅猛發展.某汽車交易市場對2017 年成交的二手車的交易前的使用時間（以下簡稱“使用時間”）進行統計，得到頻率分布直方圖如圖1.在圖1對使用時間的分組中，將使用時間落入各組的頻率視為概率.
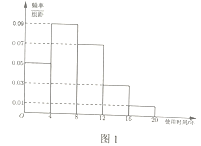
（1）記“在2017年成交的二手車中隨機選取一輛，該車的使用年限在
”，為事件
，試估計的概率；
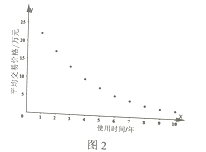
（2）根據該汽車交易市場的歷史資料，得到散點圖如圖，其中
(單位：年)表示二手車的使用時間，
（單位：萬元)表示相應的二手車的平均交易價格.
由散點圖判斷，可采用
作為二手車平均交易價格關于其使用年限的回歸方程，相關數據如下表(表中
)：
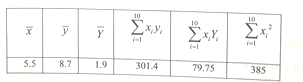
①根據回歸方程類型及表中數據，建立關于的回歸方程；
②該汽車交易市場對使用8年以內(含8年)的二手車收取成交價格
的傭金，對使用時間8年以上（不含 8年)的二手車收取成交價格
的傭金. 在圖1對使用時間的分組中，以各組的區間中點值代表該組的各個值.若以2017年的數據作為決策依據，計算該汽車交易市場對成交的每輛車收取的平均傭金.
附注：①對于一組數據
，其回歸直線
的斜率和截距的最小二乘估計分別為
，
；
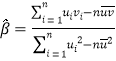②參考數據：
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，直線
的參數方程為
（
為參數）.在以原點
為極點，
軸正半軸為極軸的極坐標系中，曲線
的極坐標方程為
.
（1）求直線的極坐標方程和曲線的直角坐標方程；
（2）若直線與曲線交于
兩點，求
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
