
【題目】4月23日是“世界讀書日”,某中學開展了一系列的讀書教育活動.學校為了解高三學生課外閱讀情況,采用分層抽樣的方法從高三某班甲、乙、丙、丁四個讀書小組(每名學生只能參加一個讀書小組)學生抽取12名學生參加問卷調查.各組人數統計如下:
小組 | 甲 | 乙 | 丙 | 丁 |
人數 | 12 | 9 | 6 | 9 |
(1)從參加問卷調查的12名學生中隨機抽取2人,求這2人來自同一個小組的概率;
(2)從已抽取的甲、丙兩個小組的學生中隨機抽取2人,用![]() 表示抽得甲組學生的人數,求隨機變量
表示抽得甲組學生的人數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
【答案】(1)![]() (2)見解析,
(2)見解析, ![]()
【解析】
(1)采用分層抽樣的方法甲組抽取4人,乙組抽取3人,丙組抽取2人,丁組抽取3人,從參加問卷調查的12名學生中隨機抽取2人,基本事件總數為![]() ,這兩人來自同一小組取法共有
,這兩人來自同一小組取法共有![]() ,由此可求出所求的概率;
,由此可求出所求的概率;
(2)從已抽取的甲、丙兩個小組的學生中隨機抽取2人,而甲、丙兩個小組學生分別有4人和2 人,所以抽取的兩人中是甲組的學生的人數![]() 的可能取值為0,1,2,分別求出相應的概率,由此能求出隨機變量
的可能取值為0,1,2,分別求出相應的概率,由此能求出隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
(1)由題設易得,問卷調查從四個小組中抽取的人數分別為4,3,2,3(人),
從參加問卷調查的12名學生中隨機抽取兩名的取法![]() 共有(種),
共有(種),
抽取的兩名學生來自同一小組的取法共有![]() (種),
(種),
所以,抽取的兩名學生來自同一個小組的概率為![]()
(2)由(1)知,在參加問卷調查的12名學生中,來自甲、丙兩小組的學生人數分別為4人、2人,所以,抽取的兩人中是甲組的學生的人數![]() 的可能取值為0,1,2,
的可能取值為0,1,2,
因為![]()
![]()
![]()
所以隨機變量![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 |
|
|
|
|
所求![]() 的期望為
的期望為![]()


科目:高中數學 來源: 題型:
【題目】某公司生產某種產品的速度為![]() 千克/小時,每小時可獲得的利潤是
千克/小時,每小時可獲得的利潤是![]() 元,其中
元,其中![]() .
.
(1)要使生產該產品每小時獲得的利潤為60元,求每小時生產多少千克?
(2)要使生產400千克該產品獲得的利潤最大,問:此公司每小時應生產多少千克產品?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】20名學生某次數學考試成績(單位:分)的頻率分布直方圖如下:

(1)求頻率直方圖中a的值;
(2)分別求出成績落在[50,60)與[60,70)中的學生人數;
(3)從成績在[50,70)的學生中人選2人,求這2人的成績都在[60,70)中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著我國經濟的飛速發(fā)展,人們的生活水平也同步上升,許許多多的家庭對于資金的管理都有不同的方式.最新調查表明,人們對于投資理財的興趣逐步提高.某投資理財公司做了大量的數據調查,調查顯示兩種產品投資收益如下:
①投資A產品的收益與投資額的算術平方根成正比;
②投資B產品的收益與投資額成正比.
公司提供了投資1萬元時兩種產品的收益,分別是0.2萬元和0.4萬元.
(1)分別求出A產品的收益![]() 、B產品的收益
、B產品的收益![]() 與投資額x的函數關系式;
與投資額x的函數關系式;
(2)假如現在你有10萬元的資金全部用于投資理財,你該如何分配資金,才能讓你的收益最大?最大收益是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人獨立地對某一技術難題進行攻關。甲能攻克的概率為![]() ,乙能攻克的概率為
,乙能攻克的概率為![]() ,丙能攻克的概率為
,丙能攻克的概率為![]() .
.
(1)求這一技術難題被攻克的概率;
(2)若該技術難題末被攻克,上級不做任何獎勵;若該技術難題被攻克,上級會獎勵![]() 萬元。獎勵規(guī)則如下:若只有1人攻克,則此人獲得全部獎金
萬元。獎勵規(guī)則如下:若只有1人攻克,則此人獲得全部獎金![]() 萬元;若只有2人攻克,則獎金獎給此二人,每人各得
萬元;若只有2人攻克,則獎金獎給此二人,每人各得![]() 萬元;若三人均攻克,則獎金獎給此三人,每人各得
萬元;若三人均攻克,則獎金獎給此三人,每人各得![]() 萬元。設甲得到的獎金數為X,求X的分布列和數學期望。(本題滿分12分)
萬元。設甲得到的獎金數為X,求X的分布列和數學期望。(本題滿分12分)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩位同學參加數學應用知識競賽培訓,現分別從他們在培訓期間參加的若干次測試成績中隨機抽取8次,記錄如下:
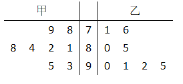
(Ⅰ)分別估計甲、乙兩名同學在培訓期間所有測試成績的平均分;
(Ⅱ)從上圖中甲、乙兩名同學高于85分的成績中各選一個成績作為參考,求甲、乙兩人成績都在90分以上的概率;
(Ⅲ)現要從甲、乙中選派一人參加正式比賽,根據所抽取的兩組數據分析,你認為選派哪位同學參加較為合適?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com