已知a∈R,求函數f(x)=x2eax的單調區間.
【答案】
分析:本題考查利用導數求函數的單調區間,這一點不是很難,但要注意對a進行分類討論
解答:解:函數f(x)的導數:f'(x)=2xe
ax+ax
2e
ax=(2x++ax
2)e
ax.
(I)當a=0時,若x<0,則f'(x)<0,若x>0,則f'(x)>0.
所以當a=0時,函數f(x)在區間(-∞,0)內為減函數,在區間(0,+∞)內為增函數.
(II)當
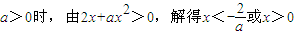
,
由
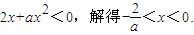
所以,當a>0時,函數f(x)在區間(-∞,-
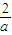
)內為增函數,在區間(-
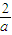
,0)內為減函數,在區間(0,+∞)內為增函數;
(III)當a<0時,由2x+ax
2>0,解得0<x<-
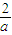
,
由2x+ax
2<0,解得x<0或x>-
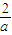
.
所以當a<0時,函數f(x)在區間(-∞,0)內為減函數,在區間(0,-
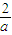
)內為增函數,在區間(-
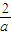
,+∞)內為減函數.
點評:本小題主要考查導數的運算,應用導數研究函數性質的方法,考查分類討論的數學思想.

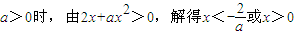 ,
,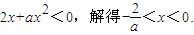
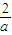 )內為增函數,在區間(-
)內為增函數,在區間(-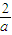 ,0)內為減函數,在區間(0,+∞)內為增函數;
,0)內為減函數,在區間(0,+∞)內為增函數;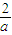 ,
,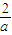 .
.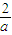 )內為增函數,在區間(-
)內為增函數,在區間(-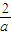 ,+∞)內為減函數.
,+∞)內為減函數.
