
【題目】已知函數![]() .
.
(Ⅰ)求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(Ⅱ)求![]() 在
在![]() 上的單調區間;
上的單調區間;
(Ⅲ)當![]() 時,證明:
時,證明:![]() 在
在![]() 上存在最小值.
上存在最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)單調遞減區間為
;(Ⅱ)單調遞減區間為![]() ,單調遞增區間為
,單調遞增區間為![]() ;(Ⅲ)詳見解析.
;(Ⅲ)詳見解析.
【解析】
(Ⅰ)先求導數,根據導數幾何意義得切線斜率,最后根據點斜式得直線方程,(Ⅱ)先求導函數在區間![]() 上零點,列表分析導函數符號變化規律,即得單調區間,(Ⅲ)利用導數研究導函數零點情況,再根據導函數零點確定函數單調性,最后根據單調性確定函數最值.
上零點,列表分析導函數符號變化規律,即得單調區間,(Ⅲ)利用導數研究導函數零點情況,再根據導函數零點確定函數單調性,最后根據單調性確定函數最值.
(Ⅰ)因為![]() ,所以
,所以![]()
則![]() ,
,![]() ,所以切線方程為
,所以切線方程為![]()
(Ⅱ)令![]() ,即
,即![]() ,
,![]() ,得
,得![]()
當![]() 變化時,
變化時,![]() 變化如下:
變化如下:
|
|
|
|
|
| 0 |
|
| 減 | 最小值 | 增 |
所以函數![]() 的單調遞減區間為
的單調遞減區間為![]() ,單調遞增區間為
,單調遞增區間為![]()
(Ⅲ)因為![]() ,所以
,所以![]()
令![]() ,則
,則![]()
因為![]() ,所以
,所以![]()
所以![]() 即
即![]() 在
在![]() 內有唯一解
內有唯一解![]()
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
所以![]() ,又因為
,又因為![]()
所以![]() 在
在![]() 內有唯一零點
內有唯一零點![]()
當![]() 時,
時,![]() 即
即![]() ,
,
當![]() 時,
時,![]() 即
即![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
所以函數![]() 在
在![]() 處取得最小值
處取得最小值
即![]() 時,函數
時,函數![]() 在
在![]() 上存在最小值
上存在最小值


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,在長方體![]() 中,點E是棱
中,點E是棱![]() 上的一個動點,若平面
上的一個動點,若平面![]() 交棱
交棱![]() 于點F,給出下列命題:
于點F,給出下列命題:
①四棱錐![]() 的體積恒為定值;
的體積恒為定值;
②對于棱![]() 上任意一點E,在棱
上任意一點E,在棱![]() 上均有相應的點G,使得
上均有相應的點G,使得![]() 平面
平面![]() ;
;
③O為底面![]() 對角線
對角線![]() 和
和![]() 的交點,在棱
的交點,在棱![]() 上存在點H,使
上存在點H,使![]() 平面
平面![]() ;
;
④存在唯一的點E,使得截面四邊形![]() 的周長取得最小值.
的周長取得最小值.
其中為真命題的是____________________.(填寫所有正確答案的序號)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點![]() ,動點
,動點![]() 在
在![]() 軸上運動,過點
軸上運動,過點![]() 作直線
作直線![]() 交
交![]() 軸于點
軸于點![]() ,延長
,延長![]() 至點
至點![]() ,使
,使![]() .
.![]() 點
點![]() 的軌跡是曲線
的軌跡是曲線![]() .
.

(1)求曲線![]() 的方程;
的方程;
(2)若![]() ,
,![]() 是曲線
是曲線![]() 上的兩個動點,滿足
上的兩個動點,滿足![]() ,證明:直線
,證明:直線![]() 過定點;
過定點;
(3)若直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,
,![]() ,求直線
,求直線![]() 的斜率
的斜率![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 經過點
經過點![]() ,離心率為
,離心率為![]() .過原點
.過原點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 有兩個不同的交點
有兩個不同的交點![]() .
.
(1)求橢圓![]() 長半軸長;
長半軸長;
(2)求![]() 最大值;
最大值;
(3)若直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,求證:
,求證:![]() 的面積與
的面積與![]() 的面積的乘積為定值.
的面積的乘積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為降低空氣污染,提高環境質量,政府決定對汽車尾氣進行整治.某廠家生產甲、乙兩種不同型號的汽車尾氣凈化器,為保證凈化器的質量,分別從甲、乙兩種型號的凈化器中隨機抽取100件作為樣本進行產品性能質量評估,評估綜合得分![]() 都在區間
都在區間![]() .已知評估綜合得分與產品等級如下表:
.已知評估綜合得分與產品等級如下表:

根據評估綜合得分,統計整理得到了甲型號的樣本頻數分布表和乙型號的樣本頻率分布直方圖(圖表如下).


甲型 乙型
(Ⅰ)從廠家生產的乙型凈化器中隨機抽取一件,估計這件產品為二級品的概率;
(Ⅱ)從廠家生產的乙型凈化器中隨機抽取3件,設隨機變量![]() 為其中二級品的個數,求
為其中二級品的個數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)根據圖表數據,請自定標準,對甲、乙兩種型號汽車尾氣凈化器的優劣情況進行比較.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某共享單車經營企業欲向甲市投放單車,為制定適宜的經營策略,該企業首先在已投放單車的乙市進行單車使用情況調查.調查過程分隨機問卷、整理分析及開座談會三個階段.在隨機問卷階段,A,B兩個調查小組分赴全市不同區域發放問卷并及時收回;在整理分析階段,兩個調查小組從所獲取的有效問卷中,針對15至45歲的人群,按比例隨機抽取了300份,進行了數據統計,具體情況如下表:
組別 年齡 | A組統計結果 | B組統計結果 | ||
經常使用單車 | 偶爾使用單車 | 經常使用單車 | 偶爾使用單車 | |
| 27人 | 13人 | 40人 | 20人 |
| 23人 | 17人 | 35人 | 25人 |
| 20人 | 20人 | 35人 | 25人 |
(1)先用分層抽樣的方法從上述300人中按“年齡是否達到35歲”抽出一個容量為60人的樣本,再用分層抽樣的方法將“年齡達到35歲”的被抽個體數分配到“經常使用單車”和“偶爾使用單車”中去.求這60人中“年齡達到35歲且偶爾使用單車”的人數;
(2)從統計數據可直觀得出“是否經常使用共享單車與年齡(記作![]() 歲)有關”的結論.在用獨立性檢驗的方法說明該結論成立時,為使犯錯誤的概率盡可能小,年齡
歲)有關”的結論.在用獨立性檢驗的方法說明該結論成立時,為使犯錯誤的概率盡可能小,年齡![]() 應取25還是35?請通過比較
應取25還是35?請通過比較![]() 的觀測值的大小加以說明.
的觀測值的大小加以說明.
參考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的準線l經過橢圓
的準線l經過橢圓![]() 的左焦點,且l與橢圓交于A,B兩點,過橢圓N右焦點
的左焦點,且l與橢圓交于A,B兩點,過橢圓N右焦點![]() 的直線交拋物線M于C,D兩點,交橢圓于G,H兩點,且
的直線交拋物線M于C,D兩點,交橢圓于G,H兩點,且![]() 面積為3.
面積為3.
(1)求橢圓N的方程;
(2)當![]() 時,求
時,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校科技小組在計算機上模擬航天器變軌返回試驗,設計方案如圖:航天器運行(按順時針方向)的軌跡方程為![]() ,變軌(即航天器運行軌跡由橢圓變為拋物線)后返回的軌跡是以
,變軌(即航天器運行軌跡由橢圓變為拋物線)后返回的軌跡是以![]() 軸為對稱軸、
軸為對稱軸、![]() 為頂點的拋物線的實線部分,降落點為
為頂點的拋物線的實線部分,降落點為![]() .觀測點
.觀測點![]() 、
、![]() 同時跟蹤航天器.
同時跟蹤航天器.
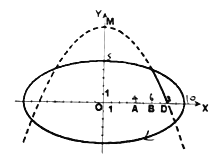
(1)求航天器變軌后的運行軌跡所在的曲線方程;
(2)試問:當航天器在![]() 軸上方時,觀測點
軸上方時,觀測點![]() 、
、![]() 測得離航天器的距離分別為多少時,應向航天器發出變軌指令?
測得離航天器的距離分別為多少時,應向航天器發出變軌指令?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com