
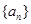 的前
的前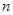 項和
項和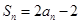 .數(shù)列
.數(shù)列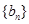 滿足:
滿足: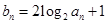 .
.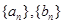 的通項
的通項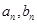 .并比較
.并比較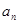 與
與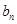 的大小;
的大小;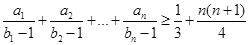 .
.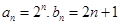 .
.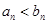 。
。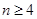 時,
時,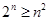
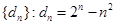 . ∵
. ∵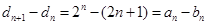
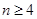 時,
時,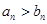 . ∴
. ∴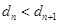 . 而
. 而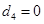 .
.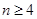 時,
時,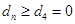 即
即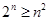 . 從而
. 從而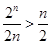 .
.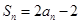 ① 當
① 當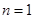 時,
時,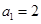 .
.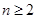 時,
時,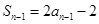 ② 由①-②有
② 由①-②有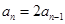 . ∵
. ∵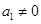
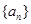 是2為首項,2為公比的等比數(shù)列. 從而
是2為首項,2為公比的等比數(shù)列. 從而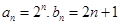 .
.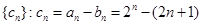
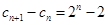 . ∴
. ∴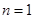 時,
時, 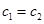 . 當
. 當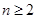 時,
時,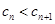
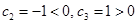 . ∴當
. ∴當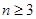 時,
時, 即
即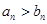 .
.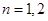 時,顯見
時,顯見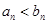
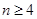 時,
時,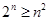
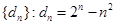 . ∵
. ∵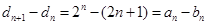
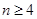 時,
時,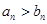 . ∴
. ∴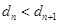 . 而
. 而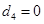 .
.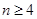 時,
時,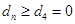 即
即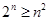 . 從而
. 從而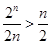 .
.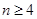 時,不等式的
時,不等式的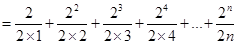
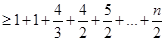
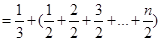
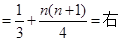
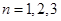 時,不等式也顯然成立.
時,不等式也顯然成立.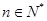 ,所證不等式均成立.
,所證不等式均成立.

 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業(yè)安徽少年兒童出版社系列答案
暑假作業(yè)安徽少年兒童出版社系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
 的公差
的公差 大于0,且
大于0,且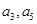 是方程
是方程 的兩根,數(shù)列
的兩根,數(shù)列 的前
的前 項和為
項和為 ,
, .
. 的通項公式;
的通項公式; 的前
的前 項和
項和 .
.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
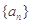 的前n項和為Sn,若a1=-15, a3+a5= -18,則當Sn取最小值時n等于( )
的前n項和為Sn,若a1=-15, a3+a5= -18,則當Sn取最小值時n等于( )| A.9 | B.8 | C.7 | D.6 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 中,
中, ,
, ,數(shù)列
,數(shù)列 中,
中, ,
, .
. 的通項公式,寫出它的前
的通項公式,寫出它的前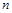 項和
項和 ;
; 的通項公式。
的通項公式。查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
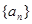 和等比數(shù)列
和等比數(shù)列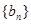 ,它們的首項是一個相等的正數(shù),且第3項也是相等的正數(shù),則
,它們的首項是一個相等的正數(shù),且第3項也是相等的正數(shù),則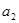 與
與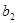 的大小關(guān)系為( )
的大小關(guān)系為( )A.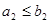 | B. | C. | D. |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com