【題目】已知一元二次函數
的圖像與
軸有兩個不同的交點,其中一個交點的坐標為
且當
時,恒有
(1)求出不等式
的解(用
表示)；
(2)若以二次函數的圖像與坐標軸的三個交點為頂點的三角形的面積為8,求
的取值范圍；
(3)若不等式
對所有
恒成立,求實數
的取值范圍.
【答案】（1）
；（2）
；（3）
.
【解析】
（1）利用
求得
關于
的表達式，進而求得不等式
的解集.
（2）根據（1）求得三個交點的坐標，利用面積列方程，求得
的表達式，進而求得的取值范圍.
（3）根據（1）中求得的表達式化簡不等式
.對
分成
三種情況進行分類討論，由此求得的取值范圍.
（1）依題意可知，即
①，由
，故①式可化為
.所以
.令
，解得
，
.由于當
時，恒有
，所以
.令
，解得
.所以不等式的解集為.
（2）結合（1）可知，三個交點的坐標為
，且.根據三角形的面積得
，化簡得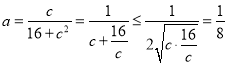
，
時等號成立，故的取值范圍是.
（3）由于，所以不等式可化為
②.
當
時，②成立.
當
時，②可化為
，而
，所以
.
當
時，②可化為
，而，所以
.
綜上所述，的取值范圍是.
科目：高中數學 來源： 題型：
【題目】橢圓的中心在原點，焦點在坐標軸上，焦距為2
.一雙曲線和該橢圓有公共焦點，且雙曲線的實半軸長比橢圓的長半軸長小4，雙曲線離心率與橢圓離心率之比為7∶3，求橢圓和雙曲線的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
的離心率為
，左頂點到直線
的距離為
．
（Ⅰ）求橢圓C的方程；
（Ⅱ）設直線
與橢圓C相交于A、B兩點，若以AB為直徑的圓經過坐標原點O，試探究：點O到直線AB的距離是否為定值？若是，求出這個定值；否則，請說明理由；
（Ⅲ）在（Ⅱ）的條件下，試求△AOB面積S的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是一景區的截面圖，
是可以行走的斜坡，已知
百米，
是沒有人行路（不能攀登）的斜坡，
是斜坡上的一段陡峭的山崖.假設你（看做一點）在斜坡上，身上只攜帶著量角器（可以測量以你為頂點的角）.
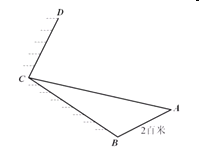
（1）請你設計一個通過測量角可以計算出斜坡的長的方案，用字母表示所測量的角，計算出的長，并化簡；
（2）設
百米，
百米，
，
，求山崖的長.（精確到米）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《九章算術》卷第五《商功》中有記載：“芻甍者，下有袤有廣，而上有袤無廣.芻，草也.甍，屋蓋也.”翻譯為“底面有長有寬為矩形，頂部只有長沒有寬為一條棱.芻甍字面意思為茅草屋頂.”現有一個芻甍，如圖，四邊形
為正方形，四邊形
、
為兩個全等的等腰梯形，
，
，若這個芻甍的體積為
，則
的長為（ ）
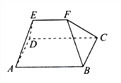
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“活水圍網”養魚技術具有養殖密度高、經濟效益好的特點.研究表明：“活水圍網”養魚時，某種魚在一定的條件下，每尾魚的平均生長速度
（單位：千克/年）是養殖密度
（單位：尾/立方米）的函數.當
時，的值為2千克/年；當
時，是的一次函數；當
時，因缺氧等原因，的值為0千克/年.
（1）當
時，求關于的函數表達式.
（2）當養殖密度為多少時，魚的年生長量（單位：千克/立方米）可以達到最大？并求出最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，曲線
的參數方程為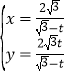
（
為參數，且
），以坐標原點為極點，
軸的正半軸為極軸建立極坐標系，已知曲線
的極坐標方程為
.
（1）將曲線的參數方程化為普通方程，并將曲線的極坐標方程化為直角坐標方程；
（2）求曲線與曲線交點的極坐標
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
