
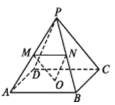
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 是邊長為2的正方形,側面
是邊長為2的正方形,側面![]() 底面
底面![]() ,
,![]() 為
為![]() 上的點,且
上的點,且![]() 平面
平面![]()
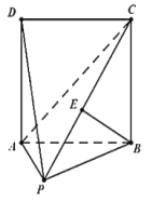
(1)求證:平面![]() 平面
平面![]() ;
;
(2)當三棱錐![]() 體積最大時,求二面角
體積最大時,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見證明;(2)![]() .
.
【解析】
(1)通過側面![]() 底面
底面![]() ,可以證明出
,可以證明出![]() 面
面![]() ,這樣可以證明出
,這樣可以證明出
![]() ,再利用
,再利用![]() 平面
平面![]() ,可以證明出
,可以證明出![]() ,這樣利用線面垂直的判定定理可以證明出
,這樣利用線面垂直的判定定理可以證明出![]() 面
面![]() ,最后利用面面垂直的判定定理可以證明出平面
,最后利用面面垂直的判定定理可以證明出平面![]() 平面
平面![]() ;
;
(2)利用三棱錐體積公式可得![]() ,
,
利用基本不等式可以求出三棱錐![]() 體積最大值,此時可以求出
體積最大值,此時可以求出![]() 的長度,以點
的長度,以點![]() 為坐標原點,以
為坐標原點,以![]() ,
,![]() 和
和![]() 分別作為
分別作為![]() 軸,
軸,![]() 軸和
軸和![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() .求出相應點的坐標,求出面
.求出相應點的坐標,求出面![]() 的一個法向量,面
的一個法向量,面![]() 的一個法向量,利用空間向量數量積的運算公式,可以求出二面角
的一個法向量,利用空間向量數量積的運算公式,可以求出二面角![]() 的余弦值.
的余弦值.
(1)證明:∵側面![]() 底面
底面![]() ,側面
,側面![]() 底面
底面![]() ,四邊形
,四邊形![]() 為正方形,∴
為正方形,∴![]() ,
,![]() 面
面![]() ,
,
∴![]() 面
面![]() ,
,
又![]() 面
面![]() ,
,
∴![]() ,
,
![]() 平面
平面![]() ,
,![]() 面
面![]() ,
,
∴![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 面
面![]() ,
,
![]() 面
面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)![]() ,
,
求三棱錐![]() 體積的最大值,只需求
體積的最大值,只需求![]() 的最大值.
的最大值.
令![]() ,由(1)知,
,由(1)知,![]() ,
,
∴![]() ,
,
而![]() ,
,
當且僅當![]() ,即
,即![]() 時,
時,
![]() 的最大值為
的最大值為![]() .
.
如圖所示,分別取線段![]() ,
,![]() 中點
中點![]() ,
,![]() ,連接
,連接![]() ,
,![]() ,
,
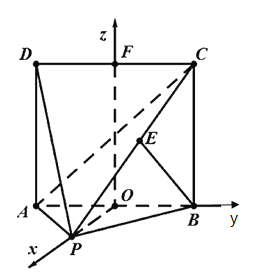
以點![]() 為坐標原點,以
為坐標原點,以![]() ,
,![]() 和
和![]() 分別作為
分別作為![]() 軸,
軸,![]() 軸和
軸和![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() .
.
由已知![]() ,
,
所以![]() ,
,
令![]() 為面
為面![]() 的一個法向量,
的一個法向量,
則有![]() ,
,
∴![]()
易知![]() 為面
為面![]() 的一個法向量,
的一個法向量,
二面角![]() 的平面角為
的平面角為![]() ,
,![]() 為銳角
為銳角
則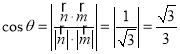 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底而ABCD是菱形,且PA=AD=2,∠PAD=∠BAD=120°,E,F分別為PD,BD的中點,且![]() .
.
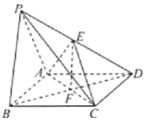
(1)求證:平面PAD⊥平面ABCD;
(2)求銳二面角E-AC-D的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】矩形ABCD中,![]() ,沿對角線AC將三角形ADC折起,得到四面體
,沿對角線AC將三角形ADC折起,得到四面體![]() ,四面體
,四面體![]() 外接球表面積為
外接球表面積為![]() ,當四面體
,當四面體![]() 的體積取最大值時,四面體
的體積取最大值時,四面體![]() 的表面積為( )
的表面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產甲、乙兩種產品,已知生產每噸甲產品要用A原料3噸,B原料2噸;生產每噸乙產品要用A原料1噸,B原料3噸.銷售每噸甲產品可獲得利潤5萬元,每噸乙產品可獲得利潤3萬元.該企業在一個生產周期內消耗A原料不超過13噸,B原料不超過18噸.
(1)列出甲、乙兩種產品滿足的關系式,并畫出相應的平面區域;
(2)在一個生產周期內該企業生產甲、乙兩種產品各多少噸時可獲得利潤最大,最大利潤是多少?
(用線性規劃求解要畫出規范的圖形及具體的解答過程)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中國詩詞大會》是央視推出的一檔以“賞中華詩詞,尋文化基因,品生活之美”為宗旨的大型文化類競賽節目,邀請全國各個年齡段、各個領域的詩詞愛好者共同參與詩詞知識比拼。“百人團”由一百多位來自全國各地的選手組成,成員上至古稀老人,下至垂髫小兒,人數按照年齡分組統計如下表:
分組(年齡) |
|
|
|
頻數(人) |
|
|
|
(1)用分層抽樣的方法從“百人團”中抽取![]() 人參加挑戰,求從這三個不同年齡組中分別抽取的挑戰者的人數;
人參加挑戰,求從這三個不同年齡組中分別抽取的挑戰者的人數;
(2)在(1)中抽出的![]() 人中,任選
人中,任選![]() 人參加一對一的對抗比賽,求這
人參加一對一的對抗比賽,求這![]() 人來自同一年齡組的概率。
人來自同一年齡組的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長均相等的四棱錐![]() 中,
中, ![]() 為底面正方形的中心,
為底面正方形的中心, ![]() ,
,![]() 分別為側棱
分別為側棱![]() ,
,![]() 的中點,有下列結論正確的有:( )
的中點,有下列結論正確的有:( )
A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() ∥平面
∥平面![]()
C.直線![]() 與直線
與直線![]() 所成角的大小為
所成角的大小為![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某學校研究性課題《什么樣的活動最能促進同學們進行垃圾分類》向題的統計圖(每個受訪者都只能在問卷的5個活動中選擇一個),以下結論錯誤的是( )

A. 回答該問卷的總人數不可能是100個
B. 回答該問卷的受訪者中,選擇“設置分類明確的垃圾桶”的人數最多
C. 回答該問卷的受訪者中,選擇“學校團委會宣傳”的人數最少
D. 回答該問卷的受訪者中,選擇“公益廣告”的人數比選擇“學校要求”的少8個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com