【答案】
分析:(1)構(gòu)造函數(shù)h(x)=f(x)-x,由已知可判斷h(x)是單調(diào)遞減函數(shù),由單調(diào)函數(shù)至多有一個(gè)零點(diǎn),及方程f(x)-x=0有實(shí)根,可證得答案;
(2)結(jié)合函數(shù)g(x)=
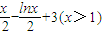
,分析條件:①方程g(x)-x=0有實(shí)根;②函數(shù)g(x)的導(dǎo)數(shù)g′(x)滿足0<g′(x)<1.兩個(gè)條件是否滿足,可得結(jié)論;
(3)不妨設(shè)α≤β,由(1)證得函數(shù)的單調(diào)性,易證明0≤f(β)-f(α)≤β-α,進(jìn)而根據(jù)絕對(duì)值的定義得到結(jié)論.
解答:證明::(1)令h(x)=f(x)-x,則h′(x)=f′(x)-1<0,故h(x)是單調(diào)遞減函數(shù),
所以,方程h(x)=0,即f(x)-x=0至多有一解,
又由題設(shè)①知方程f(x)-x=0有實(shí)數(shù)根,
所以,方程f(x)-x=0有且只有一個(gè)實(shí)數(shù)根…..(4分)
(2)易知,g′(x)=

-
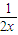
,則0<g′(x)<1,滿足條件②;
令F(x)=g(x)-x=
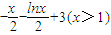
,
則F(e)=
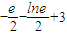
=
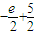
>0,F(xiàn)(e
2)=
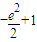
<0,…..(7分)
又F(x)在區(qū)間[e,e
2]上連續(xù),所以F(x)在[e,e
2]上存在零點(diǎn)x
,
即方程g(x)-x有實(shí)數(shù)根x
∈[e,e
2],故g(x)滿足條件①,
綜上可知,g(x)∈M…(9分)
(Ⅲ)不妨設(shè)α≤β,∵f′(x)>0,∴f(x)單調(diào)遞增,
∴f(α)≤f(β),即f(β)-f(α)≥0,,
令h(x)=f(x)-x,則h′(x)=f′(x)-1<0,故h(x)是單調(diào)遞減函數(shù),
∴f(β)-β≤f(α)-α,即f(β)-f(α)≤β-α,
∴0≤f(β)-f(α)≤β-α,
則有|f(α)-f(β)|≤|α-β|.…..….(13分)
點(diǎn)評(píng):本題是函數(shù)與方程的綜合應(yīng)用,是函數(shù)零點(diǎn)與方程根關(guān)系的綜合應(yīng)用,其中利用導(dǎo)數(shù)法分析函數(shù)的單調(diào)性,進(jìn)而判斷函數(shù)零點(diǎn)的個(gè)數(shù)及對(duì)應(yīng)方程根的個(gè)數(shù)難度較大.

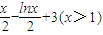 是否是集合M中的元素,并說(shuō)明理由;
是否是集合M中的元素,并說(shuō)明理由;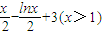 ,分析條件:①方程g(x)-x=0有實(shí)根;②函數(shù)g(x)的導(dǎo)數(shù)g′(x)滿足0<g′(x)<1.兩個(gè)條件是否滿足,可得結(jié)論;
,分析條件:①方程g(x)-x=0有實(shí)根;②函數(shù)g(x)的導(dǎo)數(shù)g′(x)滿足0<g′(x)<1.兩個(gè)條件是否滿足,可得結(jié)論; -
-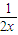 ,則0<g′(x)<1,滿足條件②;
,則0<g′(x)<1,滿足條件②;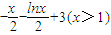 ,
,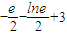 =
=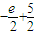 >0,F(xiàn)(e2)=
>0,F(xiàn)(e2)=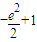 <0,…..(7分)
<0,…..(7分)

