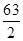已知數列
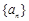
的前
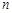
項和為
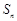
滿足
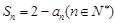
.
(Ⅰ)求數列
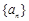
的通項公式;
(Ⅱ)求數列
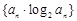
的前
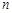
項和
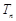
.
(Ⅰ)
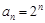
;(Ⅱ)
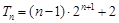
.
試題分析:(Ⅰ)
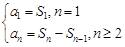
,由
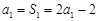
,得
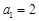
,當
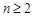
時,有
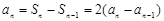
,
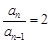
再根據等比數列的定義可求出
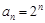
;
(Ⅱ)由(Ⅰ)可知
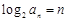
,得到
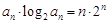
,再利用錯位相減法求
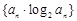
的前
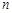
項和
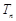
,
由題意得
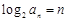
,所以
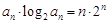
得
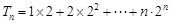
記為①,對①兩邊同時乘以數列
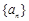
的公比2,得到②式
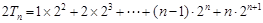
,利用錯位相減得到
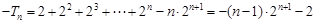
,化簡得
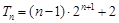
.
試題解析:(1)由
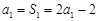
,得
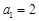
當
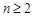
時,有
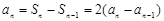
,
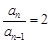
所以數列
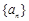
是以2為首項,2為公比的等比數列,所以
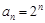
(2)由題意得
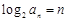
,所以
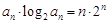
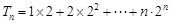
……………………………………①
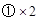
得
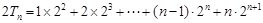
…………②
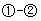
得
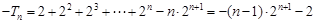
,所以
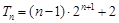
.
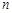
項和求法.
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
等比數列
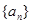
的前
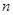
項和
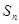
,已知
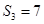
,
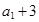
,
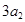
,
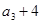
成等差數列.
(1)求數列
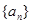
的公比
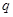
和通項
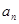
;
(2)若
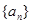
是遞增數列,令
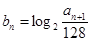
,求
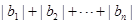
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
等比數列{
an}的前
n項和為
Sn,已知
S3=
a2+10
a1,
a5=9,則
a1 ( ).
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
已知數列{
an}為等比數列,
Sn是它的前
n項和,若
a2·
a3=2
a1,且
a4與2
a7的等差中項為
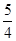
,則
S6= ( ).
| A.35 | B.33 | C.31 | D.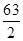 |
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
已知等比數列
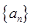
,它的前
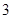
項為
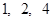
,前
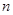
項和為
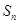
,則使得
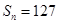
的
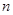
的值是( )
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
已知等比數列
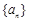
的首項為
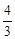
,公比為
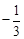
,其前
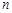
項和為
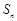
,若
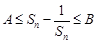
對

恒成立,則
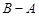
的最小值為
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
在各項都為正數的等比數列
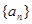
中,首項為3,前3項和為21,則
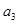
等于( )
查看答案和解析>>
主站蜘蛛池模板:
久久这里只有精品首页
|
97在线视频免费
|
国产精品精品视频
|
国产精品欧美一区二区三区
|
在线不卡二区
|
久久九九国产
|
美女视频黄又黄又免费
|
欧美日韩高清
|
色69av
|
久久精品一区二区三区四区
|
亚洲成人免费观看
|
亚洲免费视频一区二区
|
一区二区国产精品
|
久久久爽爽爽美女图片
|
日本特黄特色aaa大片免费
|
www在线看片
|
夜夜骑日日操
|
中文字幕日韩一区
|
91精品一区二区三区久久久久久
|
国产精品一区久久久久
|
亚洲人在线播放
|
国产一区二区三区在线看
|
免费黄色网址在线播放
|
国产αv在线
|
在线成人免费
|
国内久久精品视频
|
亚洲一区视频在线
|
99re6热在线精品视频播放
|
国产一级一级
|
久久一日本道色综合久久
|
深夜福利1000
|
毛片毛片毛片毛片毛片毛片
|
国产一区在线免费
|
中文字幕成人免费视频
|
97久久久
|
在线电影一区
|
国产区日韩区欧美区
|
操操网
|
日日撸夜夜操
|
日韩一区二区视频在线观看
|
国产精品久久久久久久
|

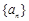 的前
的前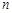 項和為
項和為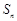 滿足
滿足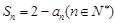 .
.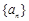 的通項公式;
的通項公式;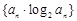 的前
的前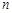 項和
項和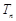 .
. 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案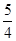 ,則S6= ( ).
,則S6= ( ).