【答案】
分析:(Ⅰ)利用x=
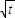
是函數的一個極值點找到數列{a
n}的遞推公式,再利用數列{a
n}的遞推公式求出數列{a
n}的通項公式即可.
(Ⅱ)先利用(Ⅰ)的結論求出數列{b
n}的通項公式,在利用裂項求和法求出數列{b
n}前n項的和為S
n,就可證明結論.
(Ⅲ)先利用(Ⅱ)的結論得出t=2時符合要求,再對t≠2時分兩種情況分別求t,看是否有符合要求的t即可.
解答:解:(Ⅰ)由題意得:f′(
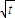
)=0即3a
n-1t-3[(t+1)a
n-a
n+1]=0
故a
n+1-a
n=t(a
n-a
n-1)(n≥2)
則當t≠1時,數列{a
n+1-a
n}是以t
2-t為首項
t為公比的等比數列
∴a
n+1-a
n=(t
2-t)t
n-1由a
n+1-a
n=a
1+(a
2-a
1)+(a
3-a
2)++(a
n-a
n-1)
=t+(t
2-t)[1+t+t
2++t
n-2]
=t+(t
2-t)•
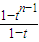
=t
n此式對t=1也成立
∴a
n=t
n(n∈N
*)(4分)
(Ⅱ)證明:由(Ⅰ)
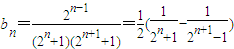
,
所以
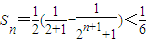
故:S
n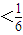
.
(Ⅲ)(1)當t=2時,由(Ⅱ)得
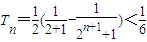
,
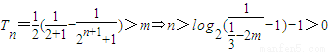
取
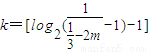
,當n≥k時,T
n>m
(2)當t<2時,
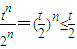
,
所以
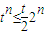
,
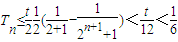
取
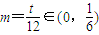
,
因為
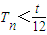
,不存在k,使得當n≥k時,T
n>m
(3)當t>2時,
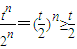
,
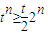
,
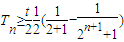
,
由(1)可知存在k∈N*,當n≥k時
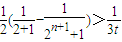
,
故存在k∈N*,當n≥k時,
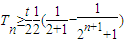
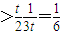
綜上,t=2
點評:本題是借助于函數的極值點來研究數列的通項以及利用裂項求和法求數列的和.是一道不太容易的題.需要綜合的知識點較多.

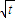 是函數f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一個極值點
是函數f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一個極值點 ,數列{bn}前n項的和為Sn,求證:Sn
,數列{bn}前n項的和為Sn,求證:Sn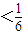
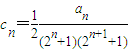 ,數列{cn}前n項的和為Tn,求同時滿足下列兩個條件的t的值:
,數列{cn}前n項的和為Tn,求同時滿足下列兩個條件的t的值: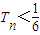
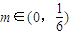 ,均存在k∈N*,當n≥k時,Tn>m.
,均存在k∈N*,當n≥k時,Tn>m.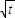 是函數的一個極值點找到數列{an}的遞推公式,再利用數列{an}的遞推公式求出數列{an}的通項公式即可.
是函數的一個極值點找到數列{an}的遞推公式,再利用數列{an}的遞推公式求出數列{an}的通項公式即可.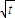 )=0即3an-1t-3[(t+1)an-an+1]=0
)=0即3an-1t-3[(t+1)an-an+1]=0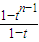 =tn
=tn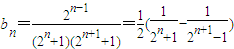 ,
,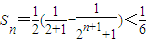
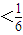 .
.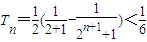 ,
,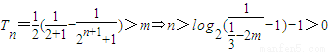
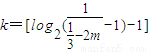 ,當n≥k時,Tn>m
,當n≥k時,Tn>m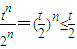 ,
,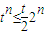 ,
,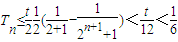
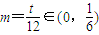 ,
,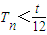 ,不存在k,使得當n≥k時,Tn>m
,不存在k,使得當n≥k時,Tn>m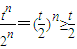 ,
,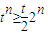 ,
,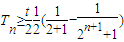 ,
,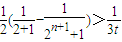 ,
,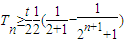


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案