
【題目】設(shè)拋物線![]() 的焦點為
的焦點為![]() ,點
,點![]() 是
是![]() 上一點,且線段
上一點,且線段![]() 的中點坐標(biāo)為
的中點坐標(biāo)為![]() .
.
(1)求拋物線![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若![]() ,
,![]() 為拋物線
為拋物線![]() 上的兩個動點(異于點
上的兩個動點(異于點![]() ),且
),且![]() ,求點
,求點![]() 的橫坐標(biāo)的取值范圍.
的橫坐標(biāo)的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)設(shè)點![]() ,由線段
,由線段![]() 的中點坐標(biāo)可得出點
的中點坐標(biāo)可得出點![]() 的坐標(biāo),再代入拋物線
的坐標(biāo),再代入拋物線![]() 的標(biāo)準(zhǔn)方程可得出關(guān)于
的標(biāo)準(zhǔn)方程可得出關(guān)于![]() 的方程,解出正數(shù)
的方程,解出正數(shù)![]() 的值,即可得出拋物線
的值,即可得出拋物線![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)點 、
、 ,求出直線
,求出直線![]() 的斜率,進(jìn)而求出直線
的斜率,進(jìn)而求出直線![]() 的方程,將直線
的方程,將直線![]() 的方程與拋物線
的方程與拋物線![]() 的標(biāo)準(zhǔn)方程聯(lián)立,可得出
的標(biāo)準(zhǔn)方程聯(lián)立,可得出![]() ,可知該方程有解,由
,可知該方程有解,由![]() 可求得
可求得![]() 的取值范圍,并進(jìn)行檢驗,由此可得出點
的取值范圍,并進(jìn)行檢驗,由此可得出點![]() 的橫坐標(biāo)的取值范圍.
的橫坐標(biāo)的取值范圍.
(1)依題意得![]() ,設(shè)
,設(shè)![]() ,由
,由![]() 的中點坐標(biāo)為
的中點坐標(biāo)為![]() ,得
,得 ,
,
即![]() ,
,![]() ,所以
,所以![]() ,得
,得![]() ,即
,即![]() ,
,
所以拋物線![]() 的標(biāo)準(zhǔn)方程為
的標(biāo)準(zhǔn)方程為![]() ;
;
(2)由題意知![]() ,設(shè)
,設(shè) ,
, ,則
,則 ,
,
因為![]() ,所以
,所以![]() ,
,![]() 所在直線方程為
所在直線方程為![]() ,
,
聯(lián)立 ,
,
因為![]() ,得
,得![]() ,即
,即![]() ,
,
因為![]() ,即
,即![]() ,故
,故![]() 或
或![]() .
.
經(jīng)檢驗,當(dāng)![]() 時,不滿足題意;
時,不滿足題意;
所以點![]() 的橫坐標(biāo)的取值范圍是
的橫坐標(biāo)的取值范圍是![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() ,
,![]() 分別為橢圓C的左、右焦點且
分別為橢圓C的左、右焦點且![]() .
.

(1)求橢圓C的方程;
(2)過P點的直線![]() 與橢圓C有且只有一個公共點,直線
與橢圓C有且只有一個公共點,直線![]() 平行于OP(O為原點),且與橢圓C交于兩點A、B,與直線
平行于OP(O為原點),且與橢圓C交于兩點A、B,與直線![]() 交于點M(M介于A、B兩點之間).
交于點M(M介于A、B兩點之間).
(i)當(dāng)![]() 面積最大時,求
面積最大時,求![]() 的方程;
的方程;
(ii)求證:![]() ,并判斷
,并判斷![]() ,
,![]() 的斜率是否可以按某種順序構(gòu)成等比數(shù)列.
的斜率是否可以按某種順序構(gòu)成等比數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
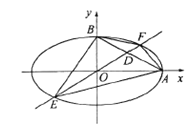
【題目】如圖,已知橢圓![]() ,點
,點![]() 是它的兩個頂點,過原點且斜率為
是它的兩個頂點,過原點且斜率為![]() 的直線
的直線![]() 與線段
與線段![]() 相交于點
相交于點![]() ,且與橢圓相交于
,且與橢圓相交于![]() 兩點.
兩點.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形![]() 的邊長為1,E,F分別是
的邊長為1,E,F分別是![]() ,
,![]() 的中點,
的中點,![]() 交EF于點D,現(xiàn)沿SE,SF及EF把這個正方形折成一個四面體,使
交EF于點D,現(xiàn)沿SE,SF及EF把這個正方形折成一個四面體,使![]() ,
,![]() ,
,![]() 三點重合,重合后的點記為G,則在四面體
三點重合,重合后的點記為G,則在四面體![]() 中必有( )
中必有( )

A.![]() 平面EFG
平面EFG
B.設(shè)線段SF的中點為H,則![]() 平面SGE
平面SGE
C.四面體![]() 的體積為
的體積為![]()
D.四面體![]() 的外接球的表面積為
的外接球的表面積為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() 且
且![]() ,點
,點![]() 在橢圓內(nèi)部,點
在橢圓內(nèi)部,點![]() 在橢圓上,則以下說法正確的是( )
在橢圓上,則以下說法正確的是( )
A.![]() 的最小值為
的最小值為![]()
B.橢圓![]() 的短軸長可能為2
的短軸長可能為2
C.橢圓![]() 的離心率的取值范圍為
的離心率的取值范圍為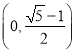
D.若![]() ,則橢圓
,則橢圓![]() 的長軸長為
的長軸長為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,焦距為
,焦距為![]() .
.
(1)求![]() 的方程;
的方程;
(2)若斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點(點
兩點(點![]() ,
,![]() 均在第一象限),
均在第一象限),![]() 為坐標(biāo)原點.
為坐標(biāo)原點.
①證明:直線![]() 的斜率依次成等比數(shù)列.
的斜率依次成等比數(shù)列.
②若![]() 與
與![]() 關(guān)于
關(guān)于![]() 軸對稱,證明:
軸對稱,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,曲線![]() 與坐標(biāo)軸的交點都在圓C上.
與坐標(biāo)軸的交點都在圓C上.
(1)求圓C的方程;
(2)若圓C與直線![]() 交于A,B兩點,且
交于A,B兩點,且![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為徹底打贏脫貧攻堅戰(zhàn),2020年春,某市政府投入資金幫扶某農(nóng)戶種植蔬菜大棚脫貧致富,若該農(nóng)戶計劃種植冬瓜和茄子,總面積不超過15畝,幫扶資金不超過4萬元,冬瓜每畝產(chǎn)量10 000斤,成本2000元,每斤售價0.5元,茄子每畝產(chǎn)量5000斤,成本3000元,每斤售價1.4元,則該農(nóng)戶種植冬瓜和茄子利潤的最大值為( )
A.4萬元B.5.5萬元C.6.5萬元D.10萬元
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某志愿者服務(wù)網(wǎng)站在線招募志愿者,當(dāng)報名人數(shù)超過計劃招募人數(shù)時,將采用隨機抽取的方法招募志愿者,如表記錄了A,B,C,D四個項目最終的招募情況,其中有兩個數(shù)據(jù)模糊,記為a,b.
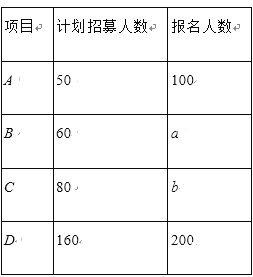
甲同學(xué)報名參加了這四個志愿者服務(wù)項目,記ξ為甲同學(xué)最終被招募的項目個數(shù),已知P(ξ=0)![]() ,P(ξ=4)
,P(ξ=4)![]() .
.
(Ⅰ)求甲同學(xué)至多獲得三個項目招募的概率;
(Ⅱ)求a,b的值;
(Ⅲ)假設(shè)有十名報了項目A的志愿者(不包含甲)調(diào)整到項目D,試判斷Eξ如何變化(結(jié)論不要求證明).
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com