【題目】F是雙曲線
1（a＞0，b＞0）的左焦點，過點F作雙曲線的一條漸近線的垂線，垂足為A，交另一條漸近線于點B．若3
，則此雙曲線的離心率為（ ）
A.2B.3C.
D.
科目：高中數學 來源： 題型：
【題目】數列{an}滿足Sn＝2n－an(n∈N*)．
(1)計算a1，a2，a3，a4，并由此猜想通項公式an；
(2)用數學歸納法證明(1)中的猜想．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本題滿分12分）已知橢圓
,直線
不過原點
且不平行于坐標軸，與
有兩個交點
，
，線段
的中點為
．
（Ⅰ）證明：直線
的斜率與的斜率的乘積為定值；
（Ⅱ）若過點
，延長線段與交于點
，四邊形
能否為平行四邊形？若能，求此時的斜率，若不能，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若對滿足條件3x+3y+8＝2xy（x＞0，y＞0）的任意x、y，（x+y）2﹣a（x+y）+16≥0恒成立，則實數a的取值范圍是（ ）
A.（﹣∞，8]B.[8，+∞）C.（﹣∞，10]D.[10，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}，{bn}滿足：a1＝3，當n≥2時，an﹣1+an＝4n；對于任意的正整數n，
．設{bn}的前n項和為Sn．
（1）求數列{an}及{bn}的通項公式；
（2）求滿足13＜Sn＜14的n的集合．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近期，長沙市公交公司推出“湘行一卡通”
掃碼支付乘車活動，活動設置了一段時間的推廣期，乘客只需利用手機下載“湘行一卡通”，再通過掃碼即可支付乘車費用.相比傳統的支付方式，掃碼支付方式極為便利，吸引了越來越多的人使用掃碼支付，某線路公交車隊統計了活動剛推出一周內每一天使用掃碼支付的人次，用
表示活動推出的天數，
表示每天使用掃碼支付的人次（單位：十人次），統計數據如下表所示：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根據以上數據，繪制了散點圖.
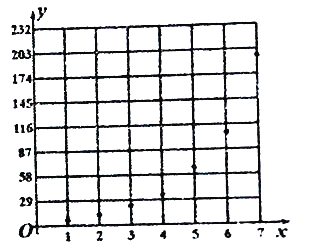
（1）根據散點圖判斷，在推廣期內，
與
（
，
均為大于零的常數）哪一個適宜作為掃碼支付的人次關于活動推出天數的回歸方程類型？（給出判斷即可，不必說明理由）；
（2）根據（1）的判斷結果及表中的數據，建立關于的回歸方程，并預測活動推出第
天使用掃碼支付的人次；
（3）推廣期結束后，車隊對乘客的支付方式進行統計，結果如下
支付方式 | 現金 | 乘車卡 | 掃碼 |
比例 |
|
|
|
假設該線路公交車票價為
元，使用現金支付的乘客無優惠，使用乘車卡付的乘客享受
折優惠，掃碼支付的乘客隨機優惠，根據統計結果得知，使用掃碼支付的乘客中有
的概率享受折優惠，有
的概率享受折優惠，有的概率享受
折優惠.根據給定數據以事件發生的頻率作為相應事件發生的概率，在不考慮其它因素的條件下，求一名乘客一次乘車的平均費用.參考數據：
|
|
|
|
|
|
|
|
|
|
其中：
，
參考公式：對于一組數據
，
，…，
…，
，其回歸直線
的斜率和截距的最小二乘估計公式分別為：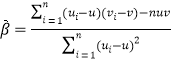
，
.
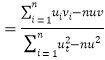查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線的中心在原點，焦點F1，F2在坐標軸上，離心率為
，且過點
．點M(3，m)在雙曲線上．
(1)求雙曲線的方程；
(2)求證：
；
(3)求△F1MF2的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設點
，
分別是橢園C：
的左、右焦點，且橢圓C上的點到的距離的最小值為
，點M，N是橢圓C上位于x軸上方的兩點，且向量
與向量
平行．
求橢圓C的方程；
當
時，求
的面積；
當
時，求直線
的方程．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
