
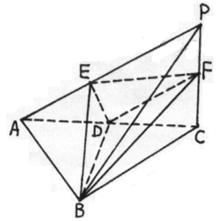
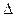 ABD和
ABD和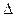 BCD均為等邊三角形,AB=2,
BCD均為等邊三角形,AB=2, AC=
AC=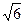 。
。
 (2)求二面角A—BC—D的大小;
(2)求二面角A—BC—D的大小;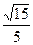
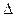 ABD為等邊三角形,O為BD的中點,∴AO垂直BD。(1分)∴ AO=CO=
ABD為等邊三角形,O為BD的中點,∴AO垂直BD。(1分)∴ AO=CO=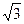 。……(2分)在
。……(2分)在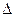 AOC中,AC=
AOC中,AC=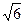 ,∴AO2+CO2=AC2,
,∴AO2+CO2=AC2,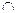 OC=O,∴AO⊥平面BCD。……(3分)
OC=O,∴AO⊥平面BCD。……(3分)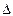 AEO中,AO=
AEO中,AO=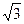 ,OE=
,OE=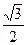 ,
,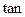 ∠
∠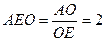 ,∴∠AEO=arctan2。
,∴∠AEO=arctan2。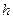 ∵VO-ACD=VA-OCD,∴
∵VO-ACD=VA-OCD,∴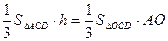 。
。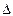 ACD中,AD=CD=2,AC=
ACD中,AD=CD=2,AC=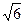 ,
,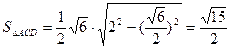 。
。
|
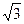 ,
,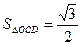 ,∴
,∴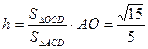 。 ∴點O到平面ACD的距離為
。 ∴點O到平面ACD的距離為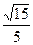 。…(13分)
。…(13分)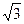 ),B(1,0,0),C(0,
),B(1,0,0),C(0,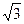 ,0),D(-1,0,0)
,0),D(-1,0,0)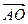 =(0,0,
=(0,0,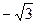 )。…(5分)
)。…(5分)
|
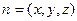 ,
, 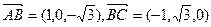 ,
,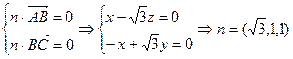 。設
。設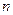 與
與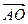 夾角為
夾角為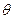 ,
,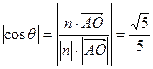 。∴二面角A—BC—D的大小為arccos
。∴二面角A—BC—D的大小為arccos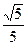 。………(8分)
。………(8分)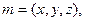 又
又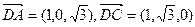
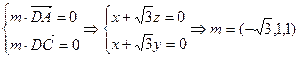 。……(11分)
。……(11分)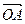 與
與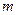 夾角為
夾角為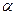 ,則
,則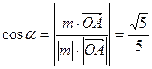 設O到平面ACD的距離為
設O到平面ACD的距離為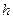 ,
,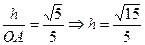 ,∴O到平面ACD的距離為
,∴O到平面ACD的距離為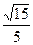 。(13分)
。(13分)

科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.如果平面 ⊥平面 ⊥平面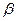 ,那么 ,那么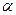 內所有直線都垂直于平面 內所有直線都垂直于平面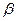 |
B.如果平面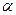 ⊥平面 ⊥平面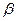 ,那么 ,那么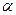 內一定存在直線平行于平面 內一定存在直線平行于平面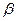 |
C.如果平面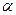 不垂直于平面 不垂直于平面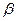 ,那么 ,那么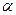 內一定不存在直線垂直于平面 內一定不存在直線垂直于平面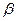 |
D.如果平面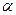 ⊥平面 ⊥平面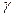 ,平面 ,平面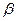 ⊥平面 ⊥平面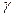 , ,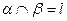 ,那么 ,那么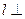 平面 平面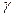 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com