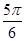(本小題滿分13分)
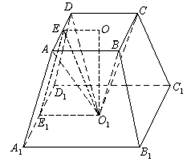
如圖,已知正方形ABCD和梯形ACEF所在的平面互相垂直,
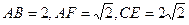
,CE//AF,
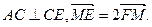
(I)求證:CM//平面BDF;
(II)求異面直線CM與FD所成角的大小;
(III)求二面角A—DF—B的大小。
(Ⅰ)見解析 (Ⅱ)
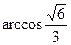
(Ⅲ)
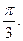
(I)證明:由題意可知CD、CB、CE兩兩垂直。
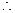
可建立如圖所示的空間直角坐標系
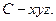
則
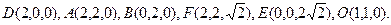
2分
由
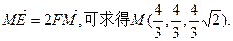
1分
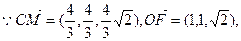
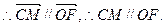
又
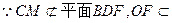
平面BDF,
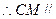
平面BDF。 2分
(Ⅱ)解:設異面直線CM與FD所成角的大小為
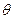
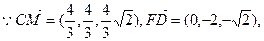
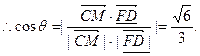
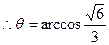
。
即異面直線CM與FD所成角的大小為
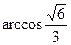
4分
(III)解:
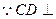
平面ADF,
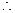
平面ADF的法向量為
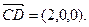
1分
設平面BDF的法向量為
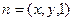
由
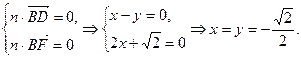
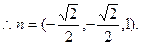
1分
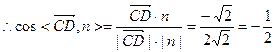
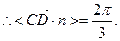
1分由圖可知二面角A—DF—B的大小為
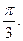
2分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
(注意:在試題卷上作答無效)
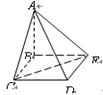
四棱錐
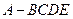
中,底面
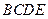
為矩形,側(cè)面
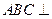
底面
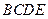
,
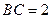
,
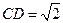
,
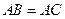
。
(Ⅰ)證明:
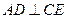
;
(Ⅱ)設
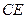
與平面
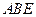
所成的角為
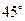
,求二面角
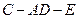
的大小。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
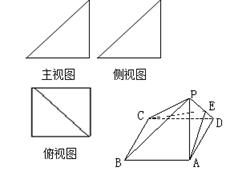
一個簡單多面體的直觀圖和三視圖如圖所示,它的主視圖和側(cè)視圖都是腰長為1的等腰直角三角形,俯視圖為正方形,E是PD的中點.
(1)求證:
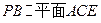
;
(2)求證:
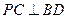
;
(3)求三棱錐
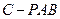
的體積.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
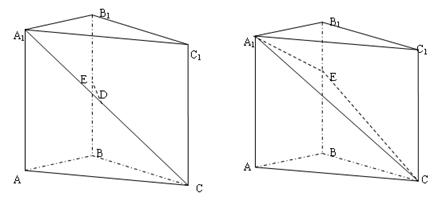
如圖直棱柱ABC-A
1B
1C
1中AB=
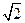
,AC=3,BC=
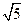
,D是A
1C的中點E是側(cè)棱BB
1上的一動點。
(1)當E是BB
1的中點時,證明:DE//平面A
1B
1C
1;
(2)求
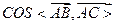
的值
(3)在棱 BB
1上是否存在點E,使二面角E-A
1C-C是直二面角?若存在求
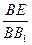
的值,不存在則說明理由。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知四棱錐P-ABCD,底面是邊長為1的正方形,側(cè)棱PC長為2,且PC⊥底面ABCD,E是側(cè)棱PC上的動點。
(Ⅰ)不論點E在何位置,是否都有BD⊥AE?證明你的結(jié)論;
(Ⅱ)求點C到平面PDB的距離;
(Ⅲ)若點E為PC的中點,求二面角D-AE-B的大小.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
正方體
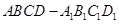
,的棱長為1,
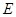
為
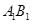
的中點,則下列五個命題:
①點
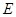
到平面
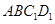
,的距離為
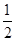
②直線
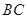
與平面
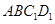
,所成的角等于
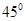
③空間四邊形
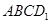
,在正方體六個面內(nèi)形成六個射影,其面積的最小值是
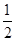
④
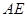
與
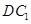
所成的角
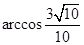
⑤二面角
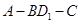
的大小為
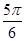
其中真命題是
。(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知直角三角形的兩直角邊長分別為3cm和4cm,則以斜邊為軸旋轉(zhuǎn)一周所得幾何體的表面積為 。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在正四棱臺內(nèi),以小底為底面。大底面中心為頂點作一內(nèi)接棱錐. 已知棱臺小底面邊長為
b,大底面邊長為
a,并且棱臺的側(cè)面積與內(nèi)接棱錐的側(cè)面面積相等,求這個棱錐的高,并指出有解的條件.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知直角梯形ABCD中,AD∥BC,AB⊥AD,∠C=45°,AD=AB=2,把梯形沿BD折起成60°的二面角C′-BD-A.求: (1)C′到平面ADB的距離;
(2)AC′與BD所成的角.
查看答案和解析>>

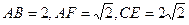 ,CE//AF,
,CE//AF,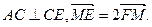
 應用題作業(yè)本系列答案
應用題作業(yè)本系列答案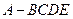 中,底面
中,底面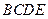 為矩形,側(cè)面
為矩形,側(cè)面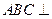 底面
底面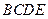 ,
,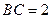 ,
,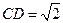 ,
,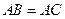 。
。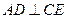 ;
;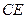 與平面
與平面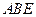 所成的角為
所成的角為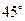 ,求二面角
,求二面角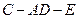 的大小。
的大小。
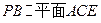 ;
;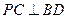 ;
; 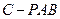 的體積.
的體積.
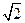 ,AC=3,BC=
,AC=3,BC=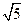 ,D是A1C的中點E是側(cè)棱BB1上的一動點。
,D是A1C的中點E是側(cè)棱BB1上的一動點。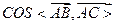 的值
的值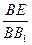 的值,不存在則說明理由。
的值,不存在則說明理由。
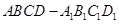 ,的棱長為1,
,的棱長為1,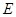 為
為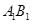 的中點,則下列五個命題:
的中點,則下列五個命題: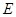 到平面
到平面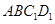 ,的距離為
,的距離為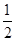
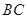 與平面
與平面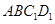 ,所成的角等于
,所成的角等于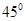
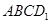 ,在正方體六個面內(nèi)形成六個射影,其面積的最小值是
,在正方體六個面內(nèi)形成六個射影,其面積的最小值是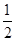
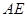 與
與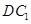 所成的角
所成的角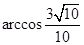
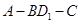 的大小為
的大小為