
(1)設點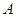 的極坐標為
的極坐標為 ,直線
,直線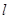 過點
過點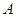 且與極軸垂直,則直線
且與極軸垂直,則直線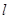 的極坐標方程為 .
的極坐標方程為 .
(2)已知函數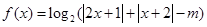 ,若關于
,若關于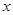 的不等式
的不等式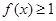 的解集為
的解集為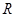 ,則
,則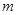 的取值范圍是 .
的取值范圍是 .
(1)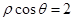 (2)
(2)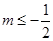
【解析】
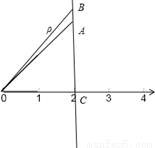
試題分析::如圖所示,設B為直線l上的任意一點,在Rt△0BC中,cosθ=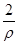 ,據此即可求出直線l的方程.如圖所示,設B為直線l上的任意一點,在Rt△0BC中,cosθ=
,據此即可求出直線l的方程.如圖所示,設B為直線l上的任意一點,在Rt△0BC中,cosθ=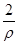 ,∴ρcosθ=2,即為直線l的極坐標方程.
,∴ρcosθ=2,即為直線l的極坐標方程.
(2)根據題意,由于函數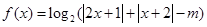 ,若關于
,若關于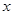 的不等式
的不等式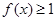 的解集為
的解集為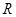 ,則可知:|2x+1|+|x+2|-m
,則可知:|2x+1|+|x+2|-m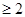 恒成立可知(|2x+1|+|x+2|-m)的最小值大于等于2即可,那么結合分段函數 最值可知
恒成立可知(|2x+1|+|x+2|-m)的最小值大于等于2即可,那么結合分段函數 最值可知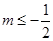
考點:極坐標方程,絕對值不等式
點評:本題考查了極坐標方程,把ρ與θ放在一個直角三角形中是常用的方法.考查絕對值不等式的應用問題,題中涉及到分類討論的思想,考查學生的靈活應用能力,屬于中檔題目.


科目:高中數學 來源: 題型:
|
| 2 |
| 3π |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| 2 |
| 3π |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| 2 |
| 3π |
| 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com