考點:定積分
專題:導(dǎo)數(shù)的概念及應(yīng)用
分析:直接利用定積分的運算法則求法求解即可.
解答:
解:
cosxdx=sinx
=1-0=1.
故選:B.
點評:本題考查定積分的運算,基本知識的考查.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
已知定義域為R的函數(shù)f(x)滿足f(-x)=-f(x+4),且當(dāng)x>2時,f(x)單調(diào)遞增,如果x1+x2<4,且(x1-2)(x2-2)<0,則下列說法正確的是( )
| A、f(x1)+f(x2)的值為正數(shù) |
| B、f(x1)+f(x2)的值為負(fù)數(shù) |
| C、f(x1)+f(x2)的值正負(fù)不能確定 |
| D、f(x1)+f(x2)的值一定為零 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
某程序框圖如圖所示,執(zhí)行該程序后輸出的S的值是( )
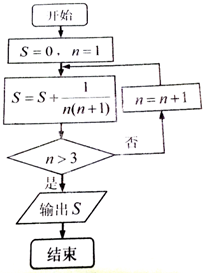
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
如果實數(shù)x、y滿足條件
,那么z=4
x•2
-y的最大值為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知函數(shù)f(x)<0定義在R上的奇函數(shù),當(dāng)x>0時,f(x)=xlnx,給出下列命題中正確命題個數(shù)是:( )
①當(dāng)x<0時,f(x)=xln(-x)
②函數(shù)f(x)有2個零點
③f(x)>0的解集為(-1,0)∪(1,+∞)
④?x
1,x
2∈[-1,1],都有|f(x
1)-f(x
2)|≤
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
復(fù)數(shù)z滿足(1+i)2•z=-1+i,其中i是虛數(shù)單位.則在復(fù)平面內(nèi),復(fù)數(shù)z對應(yīng)的點位于( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
若a,b,c是△ABC三個內(nèi)角的對邊,且asinA+bsinB=
csinC,則圓M:x
2+y
2=9被直線l:ax-by+c=0所截得的弦長為
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
設(shè)復(fù)數(shù)z
1=1+i,z
2=2+xi,(x∈R),若z
1•z
2∈R,則x的值等于
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知橢圓
+=1(a>b>0)的離心率為
,設(shè)其左、右焦點分別為F
1,F(xiàn)
2,上頂點為B
1,且F
2到直線B
1F
1的距離為
.
(Ⅰ)求橢圓的方程;
(Ⅱ)過點(2,0)作直線與橢圓交于A,B兩點,O是坐標(biāo)原點,是否存在這樣的直線,使得|
+
|=|
-
|?若存在,求出直線的方程,若不存在,試說明理由.
查看答案和解析>>

 閱讀快車系列答案
閱讀快車系列答案