Question

設a，b為異面直線，EF為a，b的公垂線，α為過EF的中點且與a，b平行的平面，M為a上任一點，N為b上任一點，求證線段MN被平面α二等分．

Answer 1

【答案】分析：過直線b作平面β∥α，過直線a及公垂線EF作一平面，在此平面內作MC∥EF，且與平面α，β分別交于B、C兩點，設EF、MN分別與平面α交于點A、D，根據中位線可得D是MN的中點．
解答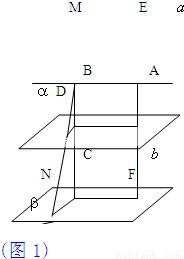：證明：過直線b作平面β∥α（如圖1）．
過直線a及公垂線EF作一平面，在此平面內作MC∥EF，且與平面α，β分別交于B、C兩點，
設EF、MN分別與平面α交于點A、D，
∵點A是EF的中點，
又ME∥BA∥CF，
∴點B是MC的中點，
又∵DB∥NC，
∴D是MN的中點．
點評：本小題主要考查平面與平面平行的性質，以及平面的基本性質及推論，考查空間想象能力、運算能力和推理論證能力，屬于基礎題．